La Ridge Regression per la regressione lineare con scikit-learn nel Machine Learning

Post Views: 355

La Ridge Regression è una tecnica di apprendimento supervisionato che aggiunge un termine di regolarizzazione chiamato “ridge penalty” alla funzione obiettivo. Questo aiuta a prevenire l’eccessiva sensibilità ai dati di addestramento, riducendo l’overfitting. La regolarizzazione Ridge è controllata da un parametro λ, che bilancia tra la riduzione della complessità del modello e la minimizzazione dell’errore.

La Ridge Regression

La Ridge Regression è stata introdotta per la prima volta da Hoerl e Kennard nel 1970 come metodo per gestire problemi di multicollinearità nei modelli di regressione lineare. Inizialmente, è stata proposta come una tecnica per migliorare le stime dei coefficienti nei casi in cui le variabili indipendenti sono fortemente correlate tra loro, causando instabilità nelle stime dei coefficienti e amplificazione della varianza.

Il nome “Ridge Regression” deriva dal fatto che il metodo aggiunge una “cresta” (in inglese, “ridge”) alla matrice di correlazione per migliorare la stabilità delle stime dei coefficienti. Questa cresta viene ottenuta attraverso l’aggiunta di un termine di regolarizzazione, noto anche come penalità L2, che consiste nella somma dei quadrati dei coefficienti moltiplicata per un parametro di regolarizzazione λ (chiamato anche alpha in alcune implementazioni come in Scikit-learn).

La Ridge Regression è diventata un’importante tecnica nel campo della statistica e dell’apprendimento automatico, in particolare per affrontare problemi di multicollinearità e overfitting nei modelli lineari. È una delle tecniche di regolarizzazione più comuni insieme alla Lasso Regression (che utilizza una penalità L1), e insieme formano la base della regressione lineare regolarizzata.

Nella Ridge Regression la funzione obiettivo da minimizzare è data da:

$J(\theta) = \sum_{i=1}^{m} (y^{(i)} - h_{\theta}(x^{(i)}))^2 + \lambda \sum_{j=1}^{n} \theta_j^2$

Dove:

( m ) è il numero di esempi nel dataset di addestramento
( n ) è il numero di caratteristiche
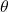$\theta$ è il vettore dei coefficienti del modello
$h_{\theta}(x)$ è la funzione ipotesi
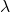$\lambda$ è il parametro di regolarizzazione (nota: tipicamente ( \lambda ) è positivo)

La regolarizzazione è rappresentata dal termine $\lambda \sum_{j=1}^{n} \theta_j^2$ , che penalizza i coefficienti $\theta$ per essere troppo grandi, limitando così la complessità del modello.

Il parametro $\lambda$ controlla l’importanza della regolarizzazione rispetto alla precisione del modello.

La Ridge Regression con scikit-learn

Ridge Regression è fornita da scikit-learn attraverso la classe Ridge per la regressione lineare. Questa classe implementa la regressione lineare con regolarizzazione Ridge utilizzando la penalità L2. Puoi utilizzare la classe Ridge per addestrare modelli di Ridge Regression e ottenere previsioni su nuovi dati. Ecco un esempio di come utilizzare la Ridge Regression con scikit-learn:

import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# Generate random data for the example
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

make_regression è una funzione di Scikit-learn che genera dati casuali per problemi di regressione. È utile per creare dataset di esempio per scopi di test, sperimentazione e dimostrazione di concetti.

Nel nostro esempio, stiamo utilizzando make_regression per generare un dataset di esempio.

n_samples: specifica il numero di campioni da generare nel dataset. In questo caso, abbiamo generato 100 campioni.
n_features: specifica il numero di caratteristiche (variabili indipendenti) da generare. Qui abbiamo generato una sola caratteristica.
noise: specifica la deviazione standard del rumore gaussiano aggiunto al target. Più alto è il valore, maggiore sarà il rumore. In questo caso, abbiamo impostato il rumore a 10.
random_state: permette di impostare il seed per la generazione casuale dei dati, garantendo che i dati generati siano riproducibili. In questo caso, abbiamo impostato il seed a 42 per motivi di riproducibilità.

make_regression restituisce due array numpy, X e y. X contiene le caratteristiche generate casualmente, mentre y contiene i corrispondenti valori target (variabili dipendenti).

In questo caso, abbiamo generato un dataset con una sola caratteristica (n_features=1) e un target associato.

Adesso possiamo dividere i dati in set di addestramento e test, addestrato un modello di Ridge Regression sui dati di addestramento e valutato le prestazioni del modello utilizzando i dati di test.

# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and train the Ridge Regression model
ridge_regression = Ridge(alpha=1.0)  # alpha is the regularization parameter (equivalent to lambda)
ridge_regression.fit(X_train, y_train)

# Make predictions on the test data
y_pred = ridge_regression.predict(X_test)

# Plot the results
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.title('Ridge Regression')
plt.xlabel('Feature')
plt.ylabel('Target')
plt.show()

Eseguendo si ottiene il seguente grafico:

Valutazione della validità del Modello

Per valutare la validità del modello di Ridge Regression creato nel codice precedente, possiamo utilizzare diverse metriche di valutazione delle prestazioni del modello. Ecco alcune metriche comuni che possiamo calcolare:

Errore Quadratico Medio (MSE): L’errore quadratico medio misura la media dei quadrati degli errori tra i valori predetti dal modello e i valori reali nel set di test. Un MSE più basso indica una migliore adattabilità del modello ai dati di test.

Coefficiente di Determinazione $R^2$ : Il coefficiente di determinazione fornisce una misura della bontà di adattamento del modello ai dati. Un valore più vicino a 1 indica un modello migliore, mentre un valore più vicino a 0 indica che il modello non è in grado di spiegare bene la variabilità dei dati.

Grafico Residui: Possiamo anche visualizzare i residui, che sono le differenze tra i valori reali e i valori predetti. Un grafico dei residui dovrebbe mostrare una distribuzione casuale intorno a zero senza un pattern evidente. Se vediamo un pattern nei residui, potrebbe indicare che il modello non è in grado di catturare completamente la struttura dei dati.

Queste sono solo alcune delle metriche che possono essere utilizzate per valutare la validità del modello. È importante utilizzare più di una metrica per ottenere una visione completa delle prestazioni del modello. Vediamo l’errore quadratico medio (MSE) e il coefficiente di determinazione del nostro modello

from sklearn.metrics import mean_squared_error, r2_score

# Calculate the mean squared error
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error:", mse)

# Calculate the coefficient of determination (R&sup2;)
r2 = r2_score(y_test, y_pred)
print("R-squared:", r2)

Eseguendo si ottengono i valori di valutazione:

Mean Squared Error: 105.78604284136125
R-squared: 0.9364639057612545

I risultati ottenuti forniscono alcune informazioni importanti sulla qualità del modello:

Mean Squared Error (MSE): 105.7

Questo valore indica la media dei quadrati degli errori tra le previsioni del modello e i valori effettivi nel set di dati di test. Un MSE più basso indica che il modello produce previsioni più accurate. Nel tuo caso, un MSE di circa 105.79 suggerisce che, in media, le previsioni del modello hanno un errore di circa 105.79 unità al quadrato rispetto ai valori reali.

Coefficient of Determination (R-squared): 0.936

Questo valore rappresenta la proporzione della varianza nei dati di risposta che è spiegata dal modello. In altre parole, è una misura di quanto bene il modello si adatta ai dati. L’R-squared può variare da 0 a 1, dove un valore più vicino a 1 indica un modello che spiega una maggiore parte della varianza nei dati. Nel tuo caso, un R-squared di circa 0.94 indica che il modello spiega circa il 94% della varianza nei dati di risposta, il che è un risultato molto buono.

Adesso passiamo alla valutazione con il grafico dei residui. Per far ciò aggiungiamo il seguente codice:

residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.axhline(y=0, color='red', linestyle='--')
plt.title('Residual Plot')
plt.show()

Eseguendo si ottiene il seguente grafico dei residui:

Lo scopo del grafico dei residui è quello di valutare se esistono problemi di eterschedasticità o omoschedasticità.

Eteroschedasticità: Si verifica quando la varianza degli errori di predizione non è costante su tutti i livelli della variabile predittiva. In pratica, significa che gli errori di predizione tendono ad essere più grandi o più piccoli a seconda dei valori delle variabili indipendenti. L’eteroschedasticità può influenzare negativamente la precisione e l’interpretazione del modello. Ad esempio, i coefficienti stimati possono essere distorti e le stime di errore possono essere inaccurate. Per affrontare l’eteroschedasticità, potresti dover trasformare le variabili o utilizzare tecniche di stima robuste che prendono in considerazione la variazione della varianza.

Omoschedasticità: Si verifica quando la varianza degli errori di predizione è costante su tutti i livelli della variabile predittiva. In questo caso, gli errori di predizione sono distribuiti uniformemente su tutti i livelli delle variabili indipendenti. La presenza di omoschedasticità è desiderabile perché rende più affidabili le stime dei parametri del modello e le previsioni. Se il modello presenta omoschedasticità, non è necessario apportare correzioni specifiche.

Nel nostro caso troviamo che nel grafico dei residui la maggior parte dei punti è sopra la linea di riferimento, questo potrebbe indicare la presenza di eteroschedasticità nei dati. Quindi, ciò suggerisce che la varianza degli errori di predizione non è costante. In questo caso, potresti voler esaminare ulteriormente i dati e considerare metodi per affrontare l’eteroschedasticità al fine di migliorare la validità del modello.

Quando usare la Ridge Regression?

La Ridge Regression è una tecnica di regressione lineare che incorpora un termine di regolarizzazione L2 per ridurre l’overfitting e migliorare la generalizzazione del modello. Ecco alcune situazioni in cui la Ridge Regression potrebbe essere preferibile rispetto ad altri metodi di regressione lineare forniti da Scikit-learn:

Multicollinearità dei predittori: Se il dataset contiene variabili predittori altamente correlate (multicollinearità), la Ridge Regression può essere preferibile perché aiuta a stabilizzare le stime dei coefficienti, evitando così l’instabilità nei coefficienti stimati che potrebbe verificarsi nella regressione lineare standard.
Controllo dell’overfitting: Quando si desidera controllare l’overfitting e prevenire la complessità eccessiva del modello, la Ridge Regression è una scelta appropriata grazie al termine di regolarizzazione L2 che limita la magnitudine dei coefficienti.
Dataset con elevata dimensionalità: In presenza di dataset con un gran numero di variabili predittori (ad alta dimensionalità), la Ridge Regression può essere preferibile perché aiuta a gestire il trade-off tra complessità del modello e adattabilità ai dati.
Stime robuste dei coefficienti: La Ridge Regression produce stime più stabili e robuste dei coefficienti rispetto alla regressione lineare standard, specialmente quando il dataset è rumoroso o contiene dati con elevata varianza.
Assenza di selezione delle caratteristiche: Se non è necessario effettuare una selezione automatica delle caratteristiche e si preferisce mantenere tutte le caratteristiche nel modello, la Ridge Regression può essere una scelta ragionevole per gestire la complessità del modello.

Tuttavia, è importante notare che la scelta del metodo di regressione dipende dalle specifiche del problema, dalla natura dei dati e dagli obiettivi dell’analisi. Altre tecniche di regressione come la regressione lineare standard, la regressione Lasso o altre forme di regolarizzazione potrebbero essere più adatte in determinati contesti. Pertanto, è consigliabile esaminare attentamente le caratteristiche del dataset e testare più modelli per determinare quale sia il più appropriato per la situazione specifica.

La Ridge Regression

La Ridge Regression con scikit-learn

Valutazione della validità del Modello

Quando usare la Ridge Regression?

Lascia un commento Annulla risposta