La Regressione: un viaggio nelle relazioni e nelle predizioni numeriche

Post Views: 316

La regressione statistica rappresenta uno strumento potente nell’arsenale degli analisti dei dati, consentendo di esplorare le relazioni tra variabili e formulare previsioni basate su queste relazioni. In questo articolo, approfondiremo la regressione, esplorando i suoi concetti fondamentali, le diverse tipologie e le applicazioni pratiche.

La regressione è una tecnica statistica che si occupa di modellare e analizzare le relazioni tra variabili. Partendo dalle basi della correlazione, la regressione va oltre, cercando di capire come una variabile dipendente cambia quando una o più variabili indipendenti variano. Questo viaggio nel cuore delle relazioni numeriche è fondamentale per fare previsioni e comprendere il mondo intorno a noi.

[wpda_org_chart tree_id=7 theme_id=50]

Tipologie di Regressione: Lineare, Multipla e non Solo

La regressione lineare è il punto di partenza. Questo modello, esplorato da Sir Francis Galton nel 1886, cerca di adattare una linea retta ai dati. Ma il mondo reale è spesso più complesso. La regressione multipla permette di considerare più di una variabile indipendente, affrontando scenari più intricati.

La regressione lineare è una tecnica semplice ma potente che cerca di modellare la relazione tra una variabile dipendente e una sola variabile indipendente attraverso una retta. L’equazione del modello è espressa come:

$Y = \beta_0 + \beta_1X + \varepsilon$

dove:

$Y$ è la variabile dipendente,
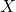$X$ è la variabile indipendente,
$\beta_0$ è l’intercetta,
$\beta_1$ è il coefficiente angolare,
$\varepsilon$ rappresenta l’errore residuo.

Il metodo dei minimi quadrati è comunemente utilizzato per stimare i coefficienti $\beta_0$ e $\beta_1$ , cercando di minimizzare la somma dei quadrati degli errori residui.

Quando la relazione tra la variabile dipendente e una sola variabile indipendente non è sufficiente, entriamo nella regressione multipla. In questo contesto, l’equazione del modello si estende per includere più variabili indipendenti:

$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_kX_k + \varepsilon$

Ogni $\beta$ rappresenta il contributo delle variabili indipendenti alla previsione della variabile dipendente. La regressione multipla offre una visione più completa delle relazioni complesse nei dati, consentendo di considerare l’effetto di più fattori simultaneamente.

Differenze Chiave tra Regressione Lineare e Multipla:

Numero di Variabili: La regressione lineare coinvolge una sola variabile indipendente, mentre la regressione multipla coinvolge più variabili indipendenti.
Complessità del Modello: La regressione multipla è più complessa, consentendo di modellare relazioni più intricate e considerare l’effetto di più fattori simultaneamente.
Interpretazione: La regressione lineare offre una chiara interpretazione della relazione tra due variabili, mentre in quella multipla, l’interpretazione può essere più sfumata a causa delle interazioni tra variabili.

In conclusione, la scelta tra regressione lineare e multipla dipende dalla complessità del fenomeno studiato e dagli obiettivi specifici dell’analisi. La regressione lineare è un punto di partenza chiaro, mentre la regressione multipla si rivela fondamentale quando le relazioni sono intrinsecamente più intricate e coinvolgono più fattori.

Altre varianti, come la regressione polinomiale o la regressione logistica, si adattano a contesti specifici, ampliando l’arsenale dell’analista. Esistono poi altre forme di regressione ancora più complesse. Tutte queste tipologie di regressione sono approfondite nella sezione Regressione Avanzata.

Come Funziona la Regressione lineare: Il Matematico dietro le Quinte

La regressione è intrisa di matematica, con il suo funzionamento basato sul principio fondamentale dei minimi quadrati. Questo metodo cerca di trovare i coefficienti del modello che minimizzano la somma dei quadrati degli errori residui, cioè le differenze tra i valori predetti dal modello e quelli effettivamente osservati. Esploriamo il cuore matematico dietro questo processo:

$Y = \beta_0 + \beta_1X + \varepsilon$

Minimizzazione della Somma dei Quadrati degli Errori Residui:

L’obiettivo è trovare i valori ottimali di (\beta_0) e (\beta_1) che riducono al minimo la somma dei quadrati degli errori residui. In forma matematica, questa somma è espressa come:

$\text{Min}\left(\sum_{i=1}^{n} \varepsilon_i^2\right)$

Dove $n$ è il numero totale di osservazioni nel nostro dataset. L’approccio utilizzato per minimizzare questa somma è noto come il Metodo dei Minimi Quadrati.

Calcolo dei Coefficienti Ottimali:

Per trovare i coefficienti ottimali, deriviamo la somma dei quadrati degli errori rispetto a $\beta_0$ e [/latex]\beta_1[/latex] e imponiamo che le derivate siano uguali a zero. Questo conduce a un sistema di equazioni chiamato “Equazioni Normali”. Le soluzioni a queste equazioni forniscono i valori ottimali di $\beta_0$ e $\beta_1$ .

Le Equazioni Normali sono date da:

$\sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i) = 0$
$\sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i)X_i = 0$

La loro risoluzione fornisce i seguenti valori ottimali:

$\beta_1 = \frac{n(\sum_{i=1}^{n} X_iY_i) - (\sum_{i=1}^{n} X_i)(\sum_{i=1}^{n} Y_i)}{n(\sum_{i=1}^{n} X_i^2) - (\sum_{i=1}^{n} X_i)^2}$

$\beta_0 = \frac{\sum_{i=1}^{n} Y_i - \beta_1(\sum_{i=1}^{n} X_i)}{n}$

Costruzione della Retta di Regressione:

Con i coefficienti ottimali in mano, possiamo costruire la retta di regressione nel piano cartesiano, rappresentando la nostra relazione predittiva tra $X$ e $Y$ .

Questa metodologia matematica fornisce una base solida per l’analisi predittiva e la modellazione delle relazioni nei dati.

Calcoliamo la regressione lineare con Python

Ecco un esempio di codice Python che implementa la regressione lineare utilizzando il Metodo dei Minimi Quadrati. Utilizzeremo la libreria numpy per le operazioni matematiche e matplotlib per la visualizzazione dei dati.

import numpy as np
import matplotlib.pyplot as plt

def regressione_lineare(X, Y):
    # Calcolo dei coefficienti ottimali
    n = len(X)
    beta_1 = (n * np.sum(X*Y) - np.sum(X) * np.sum(Y)) / (n * np.sum(X**2) - (np.sum(X))**2)
    beta_0 = (np.sum(Y) - beta_1 * np.sum(X)) / n

    return beta_0, beta_1

def retta_di_regressione(beta_0, beta_1, X):
    return beta_0 + beta_1 * X

# Dati di esempio
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 3, 4, 2, 5])

# Calcolo dei coefficienti ottimali
beta_0, beta_1 = regressione_lineare(X, Y)

# Costruzione della retta di regressione
retta_regressione = retta_di_regressione(beta_0, beta_1, X)

# Visualizzazione dei dati e della retta di regressione
plt.scatter(X, Y, label='Dati osservati')
plt.plot(X, retta_regressione, color='red', label='Retta di regressione')
plt.xlabel('Variabile Indipendente (X)')
plt.ylabel('Variabile Dipendente (Y)')
plt.legend()
plt.show()

# Stampa dei coefficienti
print(f"Coefficiente Intercezione (beta_0): {beta_0}")
print(f"Coefficiente Angolare (beta_1): {beta_1}")

Spiegazione del Codice:

La funzione regressione_lineare calcola i coefficienti ottimali (\beta_0) e (\beta_1) utilizzando il Metodo dei Minimi Quadrati.
La funzione retta_di_regressione restituisce i valori predetti della variabile dipendente utilizzando i coefficienti ottenuti.
I dati di esempio sono forniti come array numpy X e Y.
La retta di regressione viene visualizzata insieme ai dati usando matplotlib.
I coefficienti ottimali vengono stampati a schermo.

Eseguendo il codice si ottiene il risultato seguente:

Valutare la Bontà di Adattamento: R² e Altri Indicatori di Successo

Misurare quanto bene il modello di regressione si adatta ai dati è essenziale. L’indice R² (coefficiente di determinazione) fornisce una misura della proporzione di varianza nella variabile dipendente che può essere spiegata dalle variabili indipendenti. Esploriamo anche altri indicatori, come l’errore quadratico medio, che forniscono ulteriori informazioni sulla precisione delle previsioni.

Alcuni degli indicatori più comuni includono il coefficiente di determinazione $R^2$ , l’errore quadratico medio (RMSE), e l’errore percentuale assoluto medio (MAPE).

Coefficiente di Determinazione $R^2$ :

Il coefficiente $R^2$ fornisce una misura della proporzione di varianza nella variabile dipendente che è spiegata dal modello. Esso varia da 0 a 1, dove 1 indica una perfetta adattabilità. La formula è:

$R^2 = 1 - \frac{\text{Somma dei quadrati degli errori residui}}{\text{Somma totale dei quadrati}}$

Un valore più vicino a 1 suggerisce una migliore adattabilità del modello ai dati.

def calcola_R2(Y, Y_pred):
    ssr = np.sum((Y - Y_pred)**2)
    sst = np.sum((Y - np.mean(Y))**2)
    r2 = 1 - (ssr / sst)
    return r2

Errore Quadratico Medio (RMSE):

L’RMSE misura la deviazione media dei residui, cioè le differenze tra i valori predetti e quelli osservati. Una radice quadrata è applicata per portare l’errore nella stessa scala delle variabili originali.

$RMSE = \sqrt{\frac{\sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2}{n}}$

def calcola_RMSE(Y, Y_pred):
    rmse = np.sqrt(np.mean((Y - Y_pred)**2))
    return rmse

Errore Percentuale Assoluto Medio (MAPE):

Il MAPE misura l’errore percentuale medio tra i valori predetti e quelli osservati. È particolarmente utile quando si desidera valutare l’accuratezza delle previsioni in termini percentuali.

$MAPE = \frac{100}{n} \sum_{i=1}^{n} \left| \frac{Y_i - \hat{Y}_i}{Y_i} \right|$

def calcola_MAPE(Y, Y_pred):
    mape = np.mean(np.abs((Y - Y_pred) / Y)) * 100
    return mape

Questi indicatori forniscono una panoramica completa delle prestazioni del modello di regressione. Un’analisi approfondita di $R^2$ , RMSE, e MAPE aiuta a comprendere la qualità delle previsioni e se il modello è adatto al contesto specifico dei dati.

Applichiamole all’esempio in Python precedente:

def calcola_R2(Y, Y_pred):
    ssr = np.sum((Y - Y_pred)**2)
    sst = np.sum((Y - np.mean(Y))**2)
    r2 = 1 - (ssr / sst)
    return r2

def calcola_RMSE(Y, Y_pred):
    rmse = np.sqrt(np.mean((Y - Y_pred)**2))
    return rmse

def calcola_MAPE(Y, Y_pred):
    mape = np.mean(np.abs((Y - Y_pred) / Y)) * 100
    return mape

r2 = calcola_R2(Y, retta_regressione)
rmse = calcola_RMSE(Y, retta_regressione)
mape = calcola_MAPE(Y, retta_regressione)

print(f"Coefficiente di Determinazione (R^2): {r2}")
print(f"Errore Quadratico Medio (RMSE): {rmse}")
print(f"Errore Percentuale Assoluto Medio (MAPE): {mape}")

Eseguendo si ottengono i seguenti valori:

Coefficiente di Determinazione (R^2): 0.36764705882352944
Errore Quadratico Medio (RMSE): 0.9273618495495703
Errore Percentuale Assoluto Medio (MAPE): 28.199999999999996

Si vede che ili valore del coefficiente di determinazione è molto lontano dal valore 1. A questo punto si possono fare delle considerazioni. Da tale valore non si può certamente affermare che la retta ricavata con il metodo di regressione sia affidabile. I punti da cui è stata ricavata sono troppo pochi. O può essere anche che il fenomeno che stiamo osservando non ha tendenza lineare.

Limitazioni della Regressione: L’Importanza della Cautela

Mentre la regressione offre una finestra sulla comprensione delle relazioni, è fondamentale considerarne le limitazioni. L’assunzione di linearità e la presenza di variabili nascoste possono influenzare i risultati. Inoltre, l’analista deve prestare attenzione a possibili interpretazioni errate e alle implicazioni etiche dell’utilizzo dei modelli di regressione.

Assolutamente, è fondamentale comprendere le limitazioni della regressione per utilizzarla con saggezza e interpretare correttamente i risultati. Ecco alcune delle principali limitazioni della regressione:

1. Assunzioni del Modello Lineare: La regressione lineare si basa sull’assunzione che la relazione tra la variabile indipendente e la variabile dipendente sia approssimabile con una linea retta. In molti contesti, questa assunzione potrebbe non essere realistica, e modelli più complessi potrebbero essere necessari.

2. Sensibilità agli Outlier: La presenza di valori anomali (outlier) può influenzare significativamente la stima dei coefficienti di regressione, portando a modelli distorti. È importante identificare e gestire gli outlier in modo appropriato.

3. Multicollinearità: La multicollinearità si verifica quando le variabili indipendenti sono fortemente correlate tra loro. Questo può causare problemi nella stima dei coefficienti, rendendo difficile interpretare il contributo individuale di ciascuna variabile.

4. Non-linearità della Relazione: Se la relazione tra le variabili è intrinsecamente non lineare, la regressione lineare potrebbe non essere in grado di modellare accuratamente questa complessità. In tal caso, potrebbe essere necessario esplorare modelli non lineari.

5. Dipendenza dai Dati di Addestramento: I modelli di regressione possono adattarsi eccessivamente ai dati di addestramento, un fenomeno noto come overfitting. Ciò può portare a prestazioni scadenti su nuovi dati e limitare la generalizzazione del modello.

6. Assunzione degli Errori Normalmente Distribuiti: La regressione lineare assume che gli errori siano distribuiti normalmente. Se questa assunzione non è soddisfatta, potrebbe influenzare l’affidabilità degli intervalli di confidenza e dei test di ipotesi.

7. Limiti della Causalità: La regressione, per sua natura, mostra solo correlazioni e non implica necessariamente causalità. L’identificazione delle relazioni causali richiede un approccio più approfondito, come esperimenti controllati.

8. Dipendenza dai Dati di Addestramento: I modelli di regressione possono adattarsi eccessivamente ai dati di addestramento, un fenomeno noto come overfitting. Ciò può portare a prestazioni scadenti su nuovi dati e limitare la generalizzazione del modello.

Per mitigare queste limitazioni, è importante eseguire un’analisi approfondita dei dati, considerare approcci più avanzati quando necessario e valutare attentamente l’applicabilità del modello ai contesti specifici. La regressione è uno strumento potente, ma deve essere utilizzata con consapevolezza delle sue limitazioni e delle condizioni in cui è più appropriata.

Conclusione

In conclusione, la regressione è un faro nelle complessità dei dati, consentendo agli analisti di svelare relazioni e fare previsioni informate. Questo viaggio nel mondo della regressione offre solo un assaggio delle sue potenzialità, invitando gli esploratori di dati a continuare a scoprire nuove vie e applicazioni in questo vasto panorama numerico.