Si fa un grande parlare di scale musicali, di musica a 440Hz e a 432Hz senza a volta comprenderne bene il senso. In questo articolo vedremo come generare le scale musicali, la teoria che vi sta dietro, e come creare della musica a 440Hz o a 432Hz. Il tutto lo faremo utilizzando una scheda Arduino, e un piccolo speaker (o un buzzer).

La scala musicale e le frequenze corrispondenti
La musica occidentale si basa su particolari scale musicali, chiamate ottave, composte da 12 note, o per essere precisi, da 7 note intervallate (DO, RE, MI, FA, SOL, LA, SI) da 5 semitoni di passaggio (DO# o REb, RE# o MIb, FA# o SOLb, SOL# o LAb, LA# o SIb).
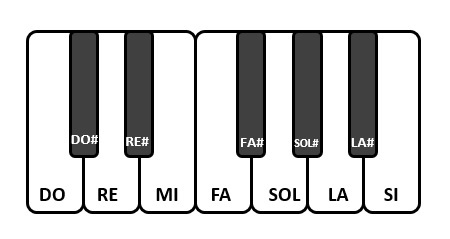
O nel sistema anglosassone le note vengono invece indicate con le prime 7 lettere dell’alfabeto, partendo però dalla nota LA (A). Si avranno quindi le note A (LA), B (SI) ,C (DO), D (RE) ,E (MI) , F (FA) e G (SOL).

E’ interessante che la notazione anglosassone parta con la nota LA. Non a caso, per convenzione, tutti gli strumenti musicali vengono accordati tenendo come frequenza di riferimento la nota LA presente sulla quarta ottava (LA4 o A4) di tutta la scala musicale. Oggi tutti gli strumenti musicali vengono accordati facendo in modo che alla nota LA4 corrisponda la frequenza 440Hz.

L’intera scala musicale è stata suddivisa in 8 scale di 12 note chiamate appunto ottave. A queste corrispondono precisi intervalli di frequenze. Per esempio l’ottava che va da LA4 a LA5 copre un intervallo di ben 440Hz, che non a caso è proprio anche la frequenza di riferimento di LA4. Quindi avremo LA4 a 440 Hz e LA5 a 880 Hz.
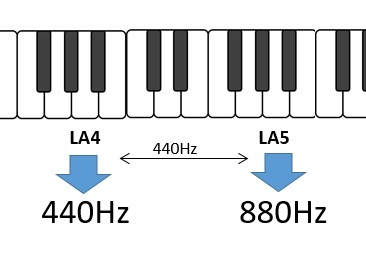
Ogni LA nell’ottava inferiore corrisponderà a metà frequenza del LA nella scala superiore, e così via per tutta la scala musicale. Quindi avremo gli intervalli di frequenze (ottave) che raddoppieranno al crescere delle ottave.
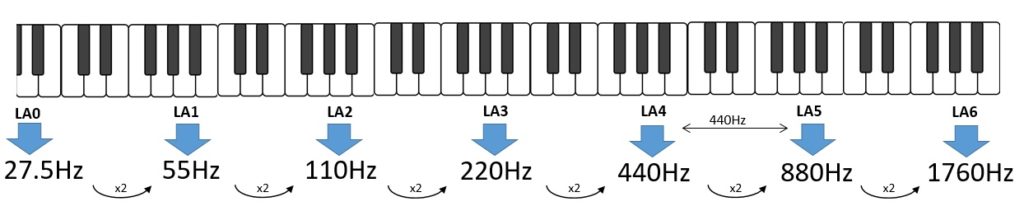
Musica a 440Hz o 432Hz?
Ma non è sempre stato così. Infatti fino a pochi decenni fa, il valore di riferimento era stato quello di 432Hz (in realtà non era l’unico). Quindi una musica a 432 Hz, non è altro che una melodia suonata con strumenti accordati su un LA4 a tale frequenza. Quindi tutti i valori delle frequenze cambieranno, ma le regole sono sempre le stesse.
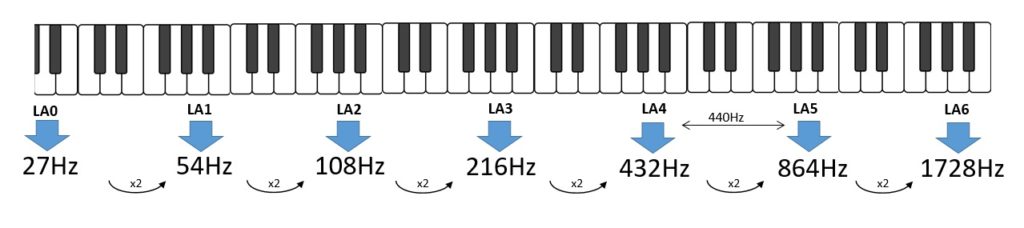
Riguardo alle motivazioni di questo cambiamento della frequenza di riferimento si fa un gran parlare sul web. Le spiegazioni disponibili non sono ben chiare, alcune delle quali risultano completamente diverse o quasi discordanti. Per poter avere una certezza su tale argomento sarebbe necessario fare una ricerca su documentazione scritta originale ed evitare assolutamente la confusione generata su web.
| Ottava | Scala a 440 Hz | Scala a 432 Hz |
|---|---|---|
| A0 | 27.5 Hz | 27 Hz |
| A1 | 55 Hz | 54 Hz |
| A2 | 108 Hz | 110 Hz |
| A3 | 220 Hz | 216 Hz |
| A4 | 440 Hz | 432 Hz |
| A5 | 880 Hz | 864 Hz |
| A6 | 1760 Hz | 1728 Hz |
| A7 | 3520 Hz | 5456 Hz |
Indipendentemente dalle motivazioni, per quanto fantasiose o corrette che siano, in questo articolo forniremo tutti gli strumenti necessari per costruire una base musicale su queste due scale (Scala a 440Hz e 432Hz), o anche su altre scale alternative, lasciando a voi il compito di sperimentare le differenze riguardo le emozioni o sensazioni suscitate.
Calcolo delle frequenze delle note
Adesso che abbiamo compreso come sono basate le scale musicali a 440Hz e 432 Hz facciamo un passo ulteriore. Una volta stabilito con quale frequenza lavorare su LA4, abbiamo visto come è facile calcolare le varie frequenze corrispondenti a tutte le altre note LA presenti sulla scala musicale. Ma all’interno di ogni ottava ci sono ben 12 note da calcolare. Come si fa?

Per il calcolo delle frequenze corrispondenti alle 12 note presenti all’interno di un’ottava esiste una particolare procedura matematica, che si basa sulla moltiplicazione della frequenza base (cioè quella del LA) per un determinato valore βn compreso tra 1 e 2, e dove n è il numero della nota corrispondente (da 0 a 12).
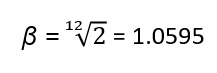
Quindi ci calcoliamo i 12 valori di β elevati alle diverse potenze con l’uso di una calcolatrice scientifica. Otterremo i seguenti valori.
| β0 | 1.0000 |
| β1 | 1.0595 |
| β2 | 1.1225 |
| β3 | 1.1893 |
| β4 | 1.2601 |
| β5 | 1.3351 |
| β6 | 1.4145 |
| β7 | 1.4986 |
| β8 | 1.5878 |
| β9 | 1.6823 |
| β10 | 1.7824 |
| β11 | 1.8884 |
| β12 | 2.0000 |
Adesso per avere le frequenze delle note comprese tra LA4 e LA5, è sufficiente moltiplicare questi valori βn per la frequenza di riferimento.
| LA4 | β0 x 440 Hz | 1.0000 x 440 Hz | 440 Hz |
| LA#4 | β1 x 440 Hz | 1.0595 x 440 Hz | 466 Hz |
| SI4 | β2 x 440 Hz | 1.1225 x 440 Hz | 494 Hz |
| DO5 | β3 x 440 Hz | 1.1893 x 440 Hz | 523 Hz |
| DO#5 | β4 x 440 Hz | 1.2601 x 440 Hz | 554 Hz |
| RE | β5 x 440 Hz | 1.3351 x 440 Hz | 587 Hz |
| RE#5 | β6 x 440 Hz | 1.4145 x 440 Hz | 622 Hz |
| MI5 | β7 x 440 Hz | 1.4986 x 440 Hz | 659 Hz |
| FA5 | β8 x 440 Hz | 1.5878 x 440 Hz | 698 Hz |
| FA#5 | β9 x 440 Hz | 1.6823 x 440 Hz | 740 Hz |
| SOL5 | β10 x 440 Hz | 1.7824 x 440 Hz | 784 Hz |
| SOL#5 | β11 x 440 Hz | 1.8884 x 440 Hz | 831 Hz |
| LA5 | β12 x 440 Hz | 2.0000 x 440 Hz | 880 Hz |
La stessa cosa la possiamo valutare per la scala musica a base 432 Hz.
| LA4 | β0 x 432 Hz | 1.0000 x 432 Hz | 432 Hz |
| LA#4 | β1 x 432 Hz | 1.0595 x 432 Hz | 458 Hz |
| SI4 | β2 x 432 Hz | 1.1225 x 432 Hz | 484 Hz |
| DO5 | β3 x 432 Hz | 1.1893 x 432 Hz | 514 Hz |
| DO#5 | β4 x 432 Hz | 1.2601 x 432 Hz | 544 Hz |
| RE | β5 x 432 Hz | 1.3351 x 432 Hz | 577 Hz |
| RE#5 | β6 x 432 Hz | 1.4145 x 432 Hz | 611 Hz |
| MI5 | β7 x 432 Hz | 1.4986 x 432 Hz | 647 Hz |
| FA5 | β8 x 432 Hz | 1.5878 x 432 Hz | 686 Hz |
| FA#5 | β9 x 432 Hz | 1.6823 x 432 Hz | 727 Hz |
| SOL5 | β10 x 432 Hz | 1.7824 x 432 Hz | 770 Hz |
| SOL#5 | β11 x 432 Hz | 1.8884 x 432 Hz | 816 Hz |
| LA5 | β12 x 432 Hz | 2.0000 x 432 Hz | 864 Hz |
Arduino e la generazione di onde sonore
Ma come fanno gli apparecchi elettronici a generare onde sonore attraverso delle casse? Apparecchi elettronici come per esempio Arduino? Bene, in realtà è molto semplice. Si collega alla nostra scheda di controllo, in questo caso Arduino, un qualsiasi dispositivo sonoro come può essere un altoparlante o un semplice buzzer. Poi attraverso dei particolari comandi lo si farà vibrare alla frequenza delle note corrispondenti.
Arduino è una scheda che permette di effettuare questa operazione in maniera davvero molto semplice. Una volta collegato il dispositivo sonoro ad una delle porte di Arduino, si comanderà a quest’ultimo di attivare e disattivare (ON e OFF) la porta in uscita alla frequenza desiderata.
Quindi dalla porta si produrrà un treno di impulsi ad onda quadra, con duty cycle del 50%.

La lunghezza in durata di tempo degli impulsi equivale alla lunghezza d’onda λ, che equivale all’inverso della frequenza 1/f. Quindi per riprodurre la nota LA4, corrispondente a 440 Hz, occorre generare un treno di impulsi con lunghezza d’onda t = 1/f = 2.2727 ms.
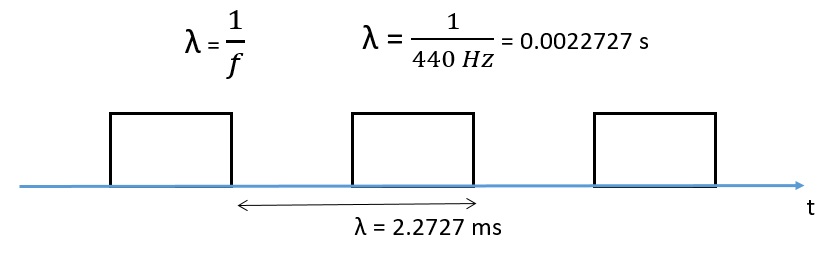
Il dispositivo sonoro sottoposto a questo treno di impulsi emetterà un perfetto LA anche se un po’ sporco, dato che l’onda generante è un’onda quadra e non un’onda sinusoidale.
Ma adesso passiamo alla programmazione, per generare l’onda quadra di cui abbiamo appena parlato sulle schede Arduino, si sceglie una porta su cui generarla, come per esempio il PIN 9, e lo impostiamo come OUTPUT
void setup() {
pinCode (3, OUTPUT)
}E poi generiamo l’onda quadra, impostando il PIN 3 sullo stato HIGH e mantenendolo per 1136 microsecondi (la metà della lunghezza d’onda), utilizzando la funzione delayMicroseconds().

Poi imposto il PIN 3 sullo stato LOW e mantenendolo ancora per 1136 microsecondi. E poi ripetendo il tutto in un loop, non si fa altro che generare un treno di impulsi, cioè l’onda quadra che abbiamo descritto sopra.
void loop() {
digitalWrite(3, HIGH)
delayMicroseconds(1136)
digitalWrite(3, LOW)
delayMicroseconds(1136)
}In questo modo otterremo la nota LA4 dal dispositivo sonoro.
Il materiale necessario
Per quanto riguarda questo articolo ho utilizzato il modello Arduino Nano della Seeeds ed il suo speaker (Grove).

Ma potete utilizzare qualsiasi modello di Arduino e collegarlo con un qualsiasi dispositivo sonoro. I principi rimarranno fondamentalmente gli stessi.
Seeeduino Nano
Seeeduino Nano è una scheda compatta completamente compatibile con Arduino Nano conservando completamente le sue stesse dimensioni e schema dei pin. Ma ci sono alcune differenze tra i due modelli.

La prima tra tutte è il prezzo, infatti Seeeduino Nano offre tutte le stesse caratteristiche di Arduino Nano, ma ad un prezzo che è all’incirca la metà. Inoltre ha alcune migliorie da non sottovalutare come per esempio la porta Mini-USB al posto della porta Type-C. Inoltre monta un connettore I2C che facilita le connessioni con molti altri componenti, e va a formare il sistema Grove dove vengono resi disponibili moltissimi sensori e attuatori che montano questo tipo di porta, facilitando le connessioni e disconnessioni senza far uso di saldature o altri formati.

Una volta scelto il sistema Grove della Seeeduino ho preso anche il particolare shield adattatore che mi permette di effettuare le connessioni con gli altri elementi del sistema Grove in maniera semplice e veloce (funziona anche con Arduino Nano).

Ed infine ho utilizzato lo Speaker del sistema Grove

Quindi, una volta a disposizione tutti i componenti non ci resta che collegarli insieme. Operazione semplicissima da eseguire con il sistema Grove.

Adesso si connette la scheda Seeeduino al computer tramite la USB e si apre l’editor Arduino IDE per poter implementare il codice, compilarlo e poi eseguirlo.
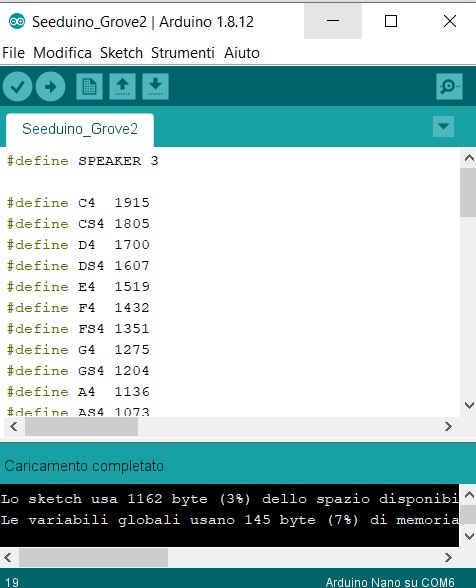
Suonare una melodia su Arduino
Una volta effettuate tutte le connessioni necessarie, si può programmare una vera e propria melodia da eseguire su Arduino. Per questo esempio ho scelto un piccolo jingle tratto dalla famosa “Per Elisa” di Beethoven, nota a tutti, anche ai profani!!!
Per prima cosa è importante definire tutte le note musicali, specificando tutte le lunghezze d’onda divise a metà per ogni nota corrispondente alla quinta e quarta ottava della scala musicale (quelle generalmente utilizzate per tutte le melodie).
#define C4 1915
#define CS4 1805
#define D4 1700
#define DS4 1607
#define E4 1519
#define F4 1432
#define FS4 1351
#define G4 1275
#define GS4 1204
#define A4 1136
#define AS4 1073
#define B4 1012
#define C5 955
#define CS5 901
#define D5 851
#define DS5 803
#define E5 758
#define F5 715
#define FS5 675
#define G5 637
#define GS5 601
#define A5 568
#define AS5 536
#define B5 506#define 12
#define 13
#define 14L’elenco delle note musicali potrete utilizzarlo anche in un altro file che poi importerete ogni volta che ne avrete bisogno. Poi si specifica il PIN a cui collegheremo il dispositivo sonoro.
#define SPEAKER 3
Poi è il momento di specificare la sequenza delle note che compongono le prime note di “Per Elisa” e la durata di ciascuna nota, attraverso due diversi array.
int BassTab[]={E5,DS5,E5,DS5,E5,B4,D5,C5,A4,C4,E4,A4,B4,E4,A4,B4,C5,E5,DS5,E5,DS5,E5,B4,D5,C5,A4,C4,E4,A4,B4,E4,C5,B4,A4};
int timeTab[]={1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,3 ,1 ,1 ,1 ,2 ,1 ,1 ,1 ,2 , 1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,3 ,1 ,1 ,1 ,2 ,1 ,1 ,1 ,4};Ed infine si passa allo sketch vero e proprio, in cui si implementano i comandi necessari per eseguire ciascuna nota rappresentata nell’array attraverso un’onda quadra con la lunghezza d’onda corrispondente a quella nota. La singola nota verrà espressa attraverso l’implementazione della funzione sound(), mentre l’esecuzione dell’intera melodia viene fatta dal ciclo for presente nel loop().
void setup()
{
pinInit();
}
void loop()
{
for(int note_index=0;note_index<34;note_index++)
{
sound(note_index);
delay(50*timeTab[note_index]);
}
}
void pinInit()
{
pinMode(SPEAKER,OUTPUT);
digitalWrite(SPEAKER,LOW);
}
void sound(uint8_t note_index)
{
for(int i=0;i<100;i++){
digitalWrite(SPEAKER,HIGH);
delayMicroseconds(BassTab[note_index]);
digitalWrite(SPEAKER,LOW);
delayMicroseconds(BassTab[note_index]);
}
}Eseguendo l’intero codice avrete l’esecuzione della melodia Per Elisa in modo continuo.
Se volete eseguire la stessa melodia su una scala musicale basata sui 432 Hz, non dovete far altro che calcolarvi le lunghezze d’onda delle note della quarta e quinta ottava e poi sostituirle allo sketch dell’articolo e provare di persona se ci sono delle differenze.
Eccovi le due ottave in 432 Hz da sostituire al codice precedente.
define C4 1946
define CS4 1838
define D4 1736
define DS4 1639
define E4 1543
define F4 1458
define FS4 1377
define G4 1299
define GS4 1225
define A4 1157
define AS4 1092
define B4 1033
define C5 973
define CS5 919
define D5 867
define DS5 818
define E5 773
define F5 729
define FS5 688
define G5 649
define GS5 613
define A5 579
define AS5 546
define B5 515