Anova, la tecnica dell’analisi della Varianza con R

Post Views: 630

Anova con R - l'analisi della varianza header

ANOVA, acronimo di “Analysis of Variance” (analisi della varianza), è una tecnica statistica utilizzata per valutare se ci sono differenze significative tra le medie di tre o più gruppi indipendenti. In altre parole, ANOVA confronta le medie di diversi gruppi per determinare se almeno uno di essi è significativamente diverso dagli altri.

La tecnica ANOVA

L’Analysis of Variance (ANOVA) è una tecnica statistica che si basa sulla decomposizione della variabilità nei dati in due componenti principali:

la variabilità tra i gruppi
la variabilità all’interno dei gruppi

Immagina di avere diverse persone assegnate a gruppi diversi e di misurare una variabile di interesse per ciascuna persona. L’ANOVA si chiede se le differenze che osserviamo tra i valori medi di queste variabili nei vari gruppi sono più grandi di quanto ci si potrebbe aspettare dalla semplice casualità.

Per fare ciò, l’ANOVA utilizza un test chiamato Test T, che confronta la varianza tra i gruppi con la varianza all’interno dei gruppi. Se la variabilità tra i gruppi è significativamente maggiore, ciò suggerisce che almeno uno dei gruppi è diverso dagli altri in termini della variabile misurata.

L’ipotesi nulla dell’ANOVA afferma che non ci sono differenze significative tra le medie dei gruppi, mentre l’ipotesi alternativa suggerisce che almeno un gruppo è significativamente diverso. La decisione di respingere o accettare l’ipotesi nulla dipende da un valore p associato al test F. Se il valore p è sufficientemente basso (generalmente sotto 0,05), si può respingere l’ipotesi nulla.

È importante notare che l’ANOVA richiede che i campioni all’interno di ciascun gruppo siano indipendenti e che le distribuzioni dei dati siano approssimativamente normali. Questi sono i principali concetti su cui si basa l’ANOVA per determinare se le differenze osservate tra i gruppi sono statisticamente significative o semplicemente dovute al caso.

Il T Test

Il test t, o t-test, è una tecnica statistica utilizzata per valutare se ci sono differenze significative tra le medie di due gruppi. Esistono diverse varianti del test t, ma le due più comuni sono il t-test per campioni indipendenti e il t-test per campioni dipendenti (o accoppiati).

Ecco come funziona ciascuna variante:

T-Test per Campioni Indipendenti:

Ipotesi Nulla e Alternativa:

Ipotesi Nulla (H0): Non ci sono differenze significative tra le medie dei due gruppi.
Ipotesi Alternativa (H1): Ci sono differenze significative tra le medie dei due gruppi.

Calcolo del t-value:

Si calcola il t-value utilizzando la differenza tra le medie dei due gruppi normalizzata per la variabilità dei dati.

$t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}$

Dove:

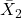$\bar{X}_1$ e $\bar{X}_2$ sono le medie dei due gruppi.
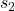$s_1$ e $s_2$ sono gli errori standard dei due gruppi.
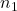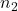$n_1$ e $n_2$ sono le dimensioni dei due campioni.

Determinazione della Significatività:

Si confronta il valore t calcolato con una distribuzione t di Student o si utilizza un software statistico per ottenere il valore p associato.

Decisione:

Se il valore p è inferiore al livello di significatività prefissato (solitamente 0,05), si può respingere l’ipotesi nulla a favore dell’ipotesi alternativa, suggerendo che ci sono differenze significative tra le medie dei due gruppi.

Libro consigliato:

Se ti piace quest’argomento, ti consiglio questo libro:

Fondamenti di Statistica per Data Scientists

T-Test per Campioni Dipendenti:

Il t-test per campioni dipendenti è utilizzato quando le misurazioni sono accoppiate, ad esempio, quando si misura la stessa cosa su individui appaiati prima e dopo un trattamento.

Il calcolo del t-value è simile, ma si considera la differenza tra le coppie di osservazioni:

$t = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}}$

Dove:

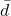$\bar{d}$ è la media delle differenze.
$s_d$ è la deviazione standard delle differenze.
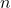$n$ è il numero di coppie di osservazioni accoppiate.

Il processo di determinazione della significatività e la decisione sono simili al t-test per campioni indipendenti.

In entrambi i casi, il test t fornisce una valutazione della probabilità che le differenze osservate tra i gruppi siano dovute al caso, e il valore p viene confrontato con il livello di significatività per prendere una decisione statistica.

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

Calcolo del valore p

Chiedo scusa per la confusione. Il calcolo del valore p in un test t implica confrontare il t-value calcolato con la distribuzione t di Student e determinare la probabilità di ottenere un t-value almeno così estremo sotto l’ipotesi nulla. Ecco come si fa:

Calcolo del t-value: Calcola il t-value usando la formula appropriata per il tipo di test t che stai eseguendo (t per campioni indipendenti o t per campioni dipendenti).
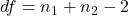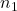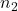Gradi di libertà: Calcola i gradi di libertà per il tuo test. Per il test t per campioni indipendenti, i gradi di libertà sono $df = n_1 + n_2 - 2$ , dove $n_1$ e $n_2$ sono le dimensioni dei due campioni. Per il test t per campioni dipendenti, i gradi di libertà sono 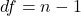$df = n - 1$ , dove 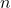$n$ è il numero di coppie di osservazioni accoppiate.
Consultazione della Distribuzione t di Student: Guarda la distribuzione t di Student con i gradi di libertà calcolati. Questa è una tabella standard o può essere ottenuta utilizzando un software statistico.
Confronto del t-value con la Tabella: Trova il valore critico della distribuzione t corrispondente al tuo livello di significatività (ad esempio, 0,05). Questo sarà il punto di taglio oltre il quale respingiamo l’ipotesi nulla.
Calcolo del Valore p: Guarda se il tuo t-value supera il valore critico. Se il t-value è più estremo (più grande o più piccolo) del valore critico, puoi calcolare il valore p come la probabilità di ottenere un t-value almeno così estremo nella distribuzione t di Student.

Calcolo di ANOVA con R

L’analisi ANOVA può essere implementata con molti linguaggi di programmazione. In R, puoi eseguire l’ANOVA utilizzando la funzione aov(). Vediamo insieme un semplice esempio. Supponiamo di avere un set di dati che contiene un fattore con tre livelli e una variabile di risposta. Ad esempio, considera il seguente set di dati fittizi:

# Creazione dei dati
set.seed(123)  # Impostiamo un seed per la riproducibilit&agrave;
gruppi <- as.factor(rep(1:3, each = 20))  # Creiamo un fattore con tre livelli
variabile_risposta <- rnorm(60, mean = c(10, 12, 15), sd = 2)  # Creiamo una variabile di risposta con medie diverse per ciascun gruppo

# Creazione del data frame
dati <- data.frame(Gruppo = gruppi, Valore = variabile_risposta)

# Visualizziamo i primi 6 righe del data frame
head(dati)

Ora che abbiamo i dati, possiamo eseguire l’ANOVA utilizzando la funzione aov():

# Eseguiamo l'ANOVA
modello_anova <- aov(Valore ~ Gruppo, data = dati)

# Visualizziamo i risultati dell'ANOVA
summary(modello_anova)

La funzione aov() crea un oggetto di tipo modello che può essere analizzato in diversi modi. La funzione summary() applicata a questo oggetto fornisce una panoramica dei risultati dell’ANOVA, inclusi i valori di F, i p-values e altre statistiche rilevanti. Eseguendo il codice otteniamo il seguente risultato:

            Df Sum Sq Mean Sq F value Pr(>F)
Gruppo       2    1.7   0.868   0.108  0.898
Residuals   57  460.4   8.077

I risultati dell’ANOVA che hai ottenuto forniscono informazioni sulla variazione spiegata e non spiegata nei tuoi dati. Ecco cosa significano le colonne:

Df (Degrees of Freedom): Questa colonna indica i gradi di libertà associati al modello. Per il tuo caso, hai due gradi di libertà per il fattore “Gruppo” e 57 gradi di libertà per gli errori (residui).
Sum Sq (Sum of Squares): Questa colonna indica la somma dei quadrati della deviazione dei dati dalla media. Per il fattore “Gruppo”, indica quanto della variazione totale nei dati può essere spiegata dalla differenza tra le medie dei diversi gruppi. Per i residui, indica la variazione non spiegata dal modello.
Mean Sq (Mean Square): Questa colonna rappresenta la media dei quadrati, calcolata dividendo la somma dei quadrati per i rispettivi gradi di libertà. È una misura della variabilità media nei dati per il fattore “Gruppo” e per i residui.
F value (F-ratio): Questo valore è il rapporto tra la variabilità spiegata e la variabilità non spiegata. Indica se le differenze tra le medie dei gruppi sono statisticamente significative. Maggiori valori di F indicano una maggiore evidenza contro l’ipotesi nulla di uguaglianza delle medie dei gruppi.
Pr(>F) (p-value): Questo valore rappresenta la probabilità di osservare un F-ratio pari o più estremo del valore osservato, supponendo che l’ipotesi nulla sia vera. Un valore di p molto piccolo (generalmente inferiore a 0.05) indica che le differenze tra le medie dei gruppi sono statisticamente significative.

Nel nostro caso, il valore di F per il fattore “Gruppo” è 0.108 con un p-value di 0.898. Questo indica che non c’è evidenza sufficiente per rifiutare l’ipotesi nulla di assenza di differenze significative tra le medie dei gruppi. In altre parole, i dati non forniscono prove significative che le medie dei gruppi siano diverse.

Se volessimo, sempre con R, visualizzare le tre distribuzioni, possiamo utilizzare il pacchetto ggplot2.

ggplot(data = dati, aes(x = Gruppo, y = Valore, color = Gruppo)) +
     geom_point() +
     labs(title = "Distribuzione dei valori per gruppo", x = "Gruppo", y = "Valore") +
     theme_minimal()

Eseguendo si ottiene il seguente grafico con la distribuzione dei punti nei 3 gruppi.

ANOVA con R - distribuzione dei vari valori per gruppo

Le diverse tipologie di ANOVA

Esistono diversi tipi di ANOVA, progettati per soddisfare le esigenze specifiche di diversi tipi di dati e design di studio. I principali tipi di ANOVA includono:

ANOVA a un fattore: Utilizzata quando c’è un solo fattore o variabile indipendente. Ad esempio, si potrebbe utilizzare per confrontare le medie di tre o più gruppi di partecipanti.
ANOVA a due fattori: Coinvolge due variabili indipendenti (fattori). Può essere suddivisa ulteriormente in ANOVA a due vie con ripetizioni (repeated measures) e senza ripetizioni.
ANOVA a più fattori: Coinvolge tre o più variabili indipendenti. È più complessa rispetto all’ANOVA a due fattori e può gestire situazioni in cui ci sono più fattori che influenzano la variabile dipendente.
ANOVA a misure ripetute: Utilizzata quando le stesse unità sperimentali sono misurate più volte. È una forma di ANOVA che tiene conto della correlazione tra le misure ripetute sullo stesso soggetto.
ANOVA multivariata (MANOVA): Estensione dell’ANOVA che coinvolge più variabili dipendenti. Viene utilizzata quando si desidera esaminare simultaneamente le differenze tra gruppi su più variabili dipendenti.
ANOVA a blocchi casualizzati: Utilizzata quando gli individui vengono suddivisi in blocchi omogenei e i trattamenti vengono assegnati casualmente all’interno di ciascun blocco.

Questi sono solo alcuni esempi e ci sono molte varianti e adattamenti specifici per diversi contesti di ricerca. La scelta del tipo di ANOVA dipende dalla natura dei dati e dalla struttura sperimentale dello studio.