La regolarizzazione è una tecnica utilizzata nell’analisi di regressione per prevenire l’overfitting e migliorare la capacità di generalizzazione del modello. L’overfitting si verifica quando il modello si adatta eccessivamente ai dati di allenamento, catturando anche il rumore nei dati anziché solo i modelli sottostanti. Questo può portare a una scarsa capacità di generalizzazione del modello su nuovi dati.
Le regolarizzazioni di Ridge e di Lasso
Consideriamo una regressione lineare standard, (OLS – Ordinary Least Squares), che si basa sui seguenti presupposti:
- Minimizza la somma dei quadrati degli errori (SQE) tra i valori predetti e i valori osservati.
- Non applica alcuna penalità ai coefficienti.
Esistono due tecniche base di Regressione Avanzata che si basano sulla regolarizzazione:
- regolarizzazione di Ridge (L2 regularization)
- regolarizzazione di Lasso (L1 regularization)
Le tecniche di Ridge Regression e Lasso Regression sono varianti della regressione lineare standard con l’aggiunta di termini di regolarizzazione per limitare la complessità del modello alla funzione obiettivo della regressione, che influisce sui coefficienti delle variabili.
La Regolarizzazione di Ridge (L2 Regularization)
Nella regolarizzazione di Ridge viene aggiunto un termine di penalizzazione proporzionale al quadrato dei valori assoluti dei coefficienti del modello (funzione obiettivo). L’obiettivo è mantenere i coefficienti piccoli ma diversi da zero. Questo aiuta a prevenire l’overfitting e a rendere il modello più stabile. La funzione obiettivo con la regolarizzazione di Ridge è data da:
dove 
è il parametro di regolarizzazione e 
sono i coefficienti del modello.
La Regolarizzazione di Lasso (L1 Regularization):
Nella regolarizzazione di Lasso, viene aggiunto un termine di penalizzazione proporzionale al valore assoluto dei coefficienti del modello (funzione obiettivo). A differenza della regolarizzazione di Ridge, la regolarizzazione di Lasso può portare alcuni coefficienti a diventare esattamente zero, rendendo il modello più interpretabile e selezionando automaticamente un sottoinsieme delle variabili. La funzione obiettivo con la regolarizzazione di Lasso è data da:
dove [late] \lambda [/latex] è il parametro di regolarizzazione e sono i coefficienti del modello.
La scelta del parametro di regolarizzazione ( \lambda ) è cruciale. Valori più elevati di aumentano la forza della penalizzazione, riducendo la complessità del modello. D’altra parte, valori troppo elevati possono portare a un modello troppo semplificato. La scelta ottimale di ( \lambda ) spesso coinvolge la validazione incrociata o altre tecniche di ottimizzazione.
In pratica, la differenza principale tra Ridge e Lasso è il tipo di norma utilizzata per penalizzare i coefficienti. Ridge utilizza la norma L2, che penalizza i coefficienti grandi senza annullarli. D’altra parte, Lasso utilizza la norma L1, che ha la proprietà di annullare alcuni coefficienti rendendoli esattamente zero. Quindi, Lasso può essere utilizzato per la selezione delle feature, mentre Ridge tende a mantenere tutti i coefficienti, anche se li riduce.
Nel tuo caso, il set di dati sintetici potrebbe non evidenziare chiaramente le differenze tra i tre modelli, poiché è stato generato con un termine quadratico. In situazioni reali con dati più complessi, è possibile che Ridge e Lasso dimostrino di essere utili nel gestire la multicollinearità e nel selezionare le feature più importanti.
Un esempio di regolarizzazione in Python
In questo esempio, stiamo generando dati sintetici con un termine quadratico per dimostrare l’efficacia della regressione polinomiale. Successivamente, suddividiamo i dati in un set di addestramento e un set di test.
Il codice include la regressione lineare standard e due tipi di regolarizzazione: Lasso (L1) e Ridge (L2). Osserviamo come i coefficienti del modello vengono influenzati dalla regolarizzazione.
Infine, la funzione plot_coefficients visualizza i coefficienti del modello dopo l’addestramento. Potrai notare che alcuni coefficienti diventano esattamente zero con Lasso, dimostrando la capacità di selezionare automaticamente le feature più rilevanti
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
# Creiamo dei dati sintetici
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + 1.5 * X**2 + np.random.randn(100, 1)
# Dividiamo i dati in training set e test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Funzione per addestrare e visualizzare il modello
def train_and_plot(model, X, y, title):
model.fit(X, y)
y_pred = model.predict(X)
plt.scatter(X, y, color='blue', label='Actual data')
plt.plot(X, y_pred, color='red', label='Model prediction')
plt.title(title)
plt.legend()
plt.show()
# Funzione per visualizzare i coefficienti del modello in forma numerica
def print_coefficients(model, title):
coefficients = model.coef_.ravel()
print(f"{title} Coefficients:")
for i, coef in enumerate(coefficients):
print(f"Coefficient {i + 1}: {coef}")
print()
# Regressione lineare standard
linear_model = LinearRegression()
train_and_plot(linear_model, X_train, y_train, 'Linear Regression')
print_coefficients(linear_model, 'Linear')
# Regressione con regolarizzazione L1 (Lasso)
lasso_model = Lasso(alpha=0.1)
train_and_plot(lasso_model, X_train, y_train, 'Lasso Regression')
print_coefficients(lasso_model, 'Lasso')
# Regressione con regolarizzazione L2 (Ridge)
ridge_model = Ridge(alpha=1.0)
train_and_plot(ridge_model, X_train, y_train, 'Ridge Regression')
print_coefficients(ridge_model, 'Ridge')Eseguendo il codice si ottengono i tre diversi grafici.
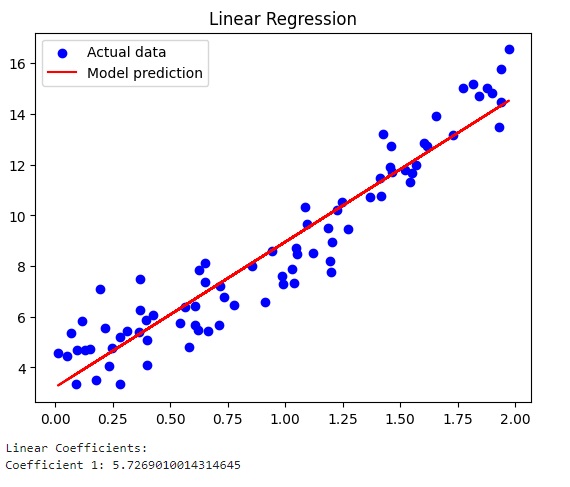
Il grafico relativo alla Regressione Lineare con il valore del coefficiente pari a 5.72
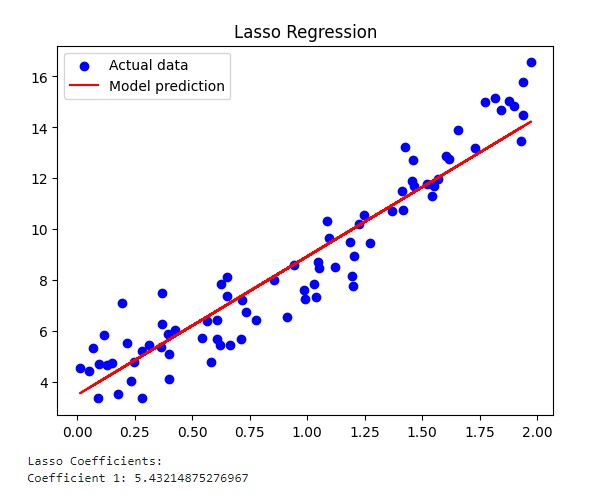
Il grafico relativo alla regolarizzazione di Lasso.
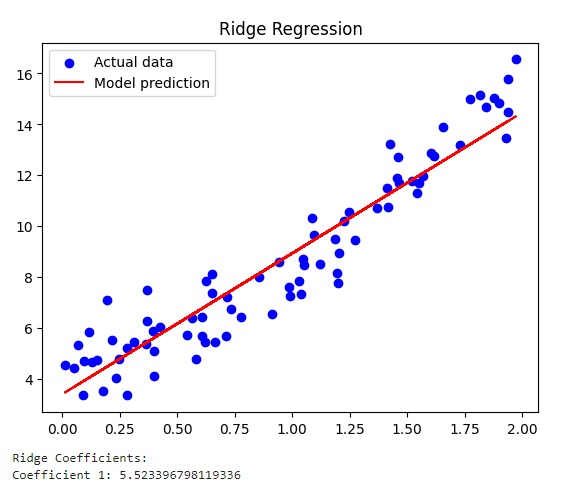
Ed infine il grafico relativo alla regolarizzazione di Ridge
