Quando si ha a che fare con un insieme di dati che descrivono una popolazione e si vogliono effettuare delle analisi statistiche, le prime caratteristiche da considerare sono la media, la mediana e la moda. Vediamo in questo articolo cosa sono e come calcolarle con R. Alla fine ci sarà qualche esempio su come visualizzarle in un grafico, come per esempio gli istogrammi e i diagrammi a candela.
La mediana
In statistica la mediana è quel determinato valore che separa un insieme di valori (popolazione) in due metà perfettamente uguali. Si potrebbe definire come il “valore di mezzo”.
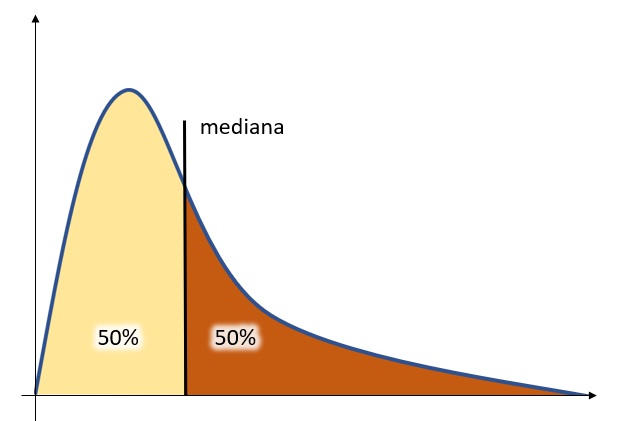
In R esiste una funzione che ci permette di calcolare la mediana in un modo molto semplice: median(). Questa funzione accetta come parametro un vettore numerico contenente tutti gli elementi della popolazione.
Per esempio, definiamo il seguente vettore:
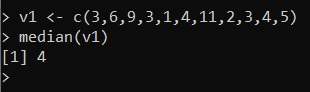
v1 <- c(3,6,9,3,1,4,11,2,3,4,5)Adesso per calcolare la mediana sarà sufficiente inserire:
median(v1)ed eseguendo si ottiene un valore pari a 4.
Ma a volte può accadere che un vettore non ha valori definiti (missing values) e quindi questi elementi riportano il valore NA. Allora se provassimo a rilanciare il comando su l’array precedente, in cui vi è presente un valore non definito:
v2 <- c(3,6,9,3,1,4,11,2,3,4,5,NA)
median(v2)purtroppo otterremo NA come risultato.

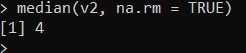
Quindi i valori definiti devono essere gestiti in qualche modo. Nella funzione median() esiste la possibilità di passare un argomento aggiuntivo, ba.rm = TRUE, che ci permette di escludere tutti i valori NA nel vettore in entrata.
median(x2, na.rm = TRUE)
Adesso, si riottiene lo stesso valore di mediana che avevamo ottenuto nel primo caso, cioè 4.
La moda
In statistica la moda è quel determinato valore di una popolazione presente in maggior numero (frequenza). Quindi è possibile anche che una popolazione di dati presenti più di una moda (due valori presenti con lo stesso maggior numero), oppure nessuna, come il caso di una popolazione distribuita uniformemente (tutti i valori sono presenti in egual numero, cioè hanno stessa frequenza).
Purtroppo in R non esiste una funzione built-in in grado di fornirci la moda di una popolazione. Sarà quindi necessario creare una funzione che lo faccia. Questa semplice funzione funziona solo nel caso in cui la moda sia unica (cioè che la moda sia unica, altrimenti restituisce la prima moda che trova).
moda <- function(v) {
tmp <- unique(v)
uniqv[which.max(tabulate(match(v, tmp)))]
}Se usiamo lo stesso vettore di elementi utilizzato nell’esempio precedente:
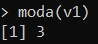
v1 <- c(3,6,9,3,1,4,11,2,3,4,5)adesso saremo in grado di calcolare la moda:
moda(v1)ed eseguendo si ottiene un valore pari a 3, che in effetti è il valore con frequenza maggiore all’interno del vettore.
Adesso non ci rimane che vedere come calcolare la media della popolazione
La media
La media è la somma di tutti i valori di una popolazione diviso il numero di elementi che la compongono.
Il calcolo della media è un’operazione molto comune, e quindi non poteva non essere presenta anche in R. Si utilizza la funzione mean() per calcolare la media di un vettore di elementi passato come argomento.
Considerando sempre lo stesso vettore degli altri esempi:
v1 <- c(3,6,9,3,1,4,11,2,3,4,5)La media sarà facilmente calcolabile scrivendo:
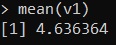
mean(v1)ed eseguendo si ottiene un valore pari a 4,636364.
Calcoliamo la mediana, la moda e la media su un dataframe
Finora abbiamo visto come esempio più basilare il calcolo della mediana, della moda e della media su un vettore di elementi. Spesso, quando si ha a che fare con dati da studiare abbiamo dei dati raccolti sotto forma di dataframe. Per creare un dataframe, si specificano dapprima le colonne come vettori e poi si uniscono formato la tabella (dataframe).
age <- c(12,33,22,41,31,27,17,14,28,35)
gender <- c('W','M','M','W','M','M','W','W','W','M')
df <- data.frame(age, gender)Eseguendo si ottiene un dataframe con i valori specificati all’interno dei vettori come colonne:
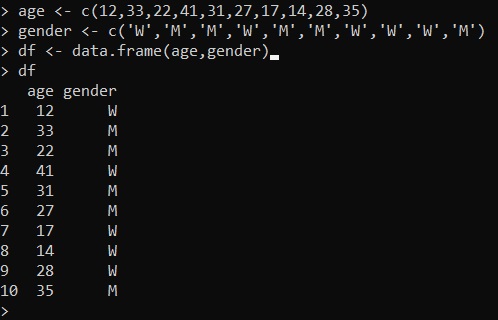
Anche in questo caso è possibile calcolare la mediana, per i valori in colonna
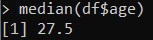
median(df$age)e troveremo il valore di 27.5
Stessa cosa per la moda e la media
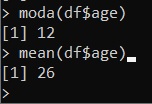
moda(df$age)
mean(df$age)eseguendo i comandi uno alla volta si ottengono i seguenti valori:
Un ulteriore passo in avanti sarà quello di calcolare la mediana (o la media e la moda) in base al gruppo di appartenenza. Se controllate il dataframe che abbiamo specificato, abbiamo una serie di età di individui in cui nella seconda colonna è specificato il genere (W =woman e M = man).
Bene è possibile calcole due mediane in base al sesso di appartenza dei due gruppi. Per fare questo si combina la funzione aggregate() con la funzione della mediana nel seguente modo:
aggregate(df$age, list(df$gender), median)In questo modo si ottiene una mediana per ciascun sesso di appartenza, 31 per gli uomini e 17 per le donne.
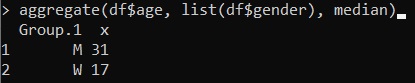
Stessa cosa per il calcolo della moda e della media:
aggregate(df$age, list(df$gender), median)
aggregate(df$age, list(df$gender), mean)Eseguendo i due comandi uno alla volta si ottengono i seguenti valori:

Adesso che abbiamo visto come poter calcolare questi valori sarebbe una buona idea vedere come poterli visualizzare in un grafico.
Visualizzare la mediana
Adesso che abbiamo visto la mediana, ci piacerebbe vedere qualche modo per poterla visualizzare. Generalmente la mediana viene visualizzata in grafici di distribuzione di popolazioni che possono essere dei diagrammi a candele (boxplot) o più generalmente, degli istogrammi.
Per aiutarci meglio nella nostra rappresentazione di esempio, genereremo un dataset con un numero elevato di elementi. Possiamo utilizzare un generatore casuale di elementi di una distribuzione di Poisson, la funzione rpois(). Inseriamo anche un valore preciso come seme per ottenere sempre gli stessi valori casuali.
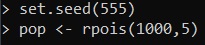
set.seed(555)
pop <- rpois(1000, 5)A questo punto abbiamo creato una distribuzione di Poisson di 1000 elementi aventi per valore medio 5 (lambda).
Calcoliamone la mediana, come sappiamo fare:
median(pop)e troveremo il valore di 5, dato in una distribuzione di Poisson la moda è uguale al valore di lambda passato nella costruzione della distribuzione casuale.

Allo stesso modo possiamo calcolare la media e la moda:
mean(pop)
moda(pop)Eseguendo i comandi uno alla volta otterremo i seguenti valori:
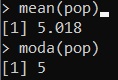
Adesso visualizziamo la distribuzione di Poisson generata sotto forma di un diagramma a candela. In questo caso i giochi sono davvero semplici….nella visualizzazione di un diagramma a candela la mediana viene già evidenziata tramite una riga nera.
boxplot(pop)Infatti in corrispondenza del valore 5 avremo una linea orizzontale marcata.

Ma se volessimo aggiungere una riga in corrispondenza della media, allora dovremo aggiungere:
boxplot(pop)
abline(h= mode(pop2), col = "blue", lwd=3)
Per quanto riguarda invece la visualizzazione degli istogrammi, dovremo noi aggiungere una linea in corrispondenza della mediana, e la marcheremo con il colore blu. Con la funzione abline() è possibile disegnare una linea direttamente sopra l’istogramma.
hist(pop)
abline(v = median(pop), col = "blue", lwd = 3)
In questo caso media, moda e mediana si sovrapporrebbero nella visualizzazione, ma nulla vieta in altri casi di aggiungere altre linee in loro corrispondenza utilizzando colori diversi.
