La Serie di Fibonacci: tre diversi algoritmi a confronto

Pubblicato il di
Post Views: 717
La serie di Fibonacci, tre algoritmi a confronto header

L’efficienza degli algoritmi riveste un ruolo centrale nello sviluppo di software, influenzando direttamente le prestazioni e la responsività delle applicazioni. In questo contesto, la serie di Fibonacci fornisce un terreno fertile per esplorare e confrontare diverse strategie di implementazione, dal classico approccio ricorsivo a soluzioni più ottimizzate come l’iterazione e la programmazione dinamica.

[wpda_org_chart tree_id=42 theme_id=50]

Questo articolo si propone di analizzare tre approcci principali per generare la serie di Fibonacci in Python: l’implementazione ricorsiva, l’approccio iterativo e quello basato sulla programmazione dinamica. Attraverso il confronto delle complessità asintotiche e l’analisi pratica delle prestazioni, cercheremo di evidenziare le caratteristiche distintive di ciascun metodo e fornire indicazioni sulla scelta dell’algoritmo più adatto a specifici scenari.

Il processo decisionale nell’adozione di un algoritmo risulta cruciale per garantire un’ottimizzazione delle risorse e una risposta efficiente ai requisiti del problema. Invitiamo dunque alla scoperta attiva di soluzioni ottimizzate, sottolineando l’importanza della sperimentazione e della comprensione del contesto applicativo per prendere decisioni informate nella progettazione e nell’implementazione di algoritmi.

La serie di Fibonacci

La serie di Fibonacci è una sequenza di numeri interi in cui ogni numero è la somma dei due precedenti, iniziando con 0 e 1. La sequenza è così definita:

F(0) = 0, \quad F(1) = 1

F(n) = F(n-1) + F(n-2) \quad \text{per } n > 1

La sequenza inizia con 0, 1, 1, 2, 3, 5, 8, 13, 21, e così via. Ogni numero successivo è la somma dei due numeri precedenti. La sequenza è stata introdotta in Europa da Leonardo Fibonacci nel suo libro “Liber Abaci” nel 1202, ma la sequenza era già nota in India molto prima.

La serie di Fibonacci mostra diverse proprietà matematiche interessanti. Alcune di esse includono:

  • Proprietà di Ricorrenza:
    F(n) = F(n-1) + F(n-2)
  • Limite Asintotico:
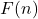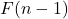    Con l’aumentare di (n), il rapporto tra F(n) e F(n-1) converge al rapporto aureo \phi \approx 1.6180339887, noto come la sezione aurea.
  • Formula Chiusa:
    Esiste una formula chiusa per calcolare l’n-esimo numero di Fibonacci utilizzando la sezione aurea:
    F(n) = \frac{\phi^n - (1-\phi)^n}{\sqrt{5}}

Dove \phi è il rapporto aureo, approssimato a circa 1.6180339887.

La serie di Fibonacci ha una presenza notevole sia in matematica che in informatica. In matematica, la sequenza si manifesta in numerosi fenomeni naturali, come la disposizione delle foglie su un ramo, i petali dei fiori e la spirale di alcune conchiglie. Inoltre, la serie di Fibonacci è correlata al concetto di sezione aurea, con il rapporto tra i numeri successivi convergente al valore approssimato di 1.6180339887.

In informatica, la serie di Fibonacci è spesso utilizzata come esempio per illustrare concetti fondamentali come la ricorsione, la programmazione dinamica e la complessità algoritmica. Gli algoritmi per generare la serie di Fibonacci forniscono un terreno fertile per esplorare diverse strategie di risoluzione di problemi e ottimizzazione.

La sua presenza ubiqua in natura e la sua rilevanza nell’informatica fanno della serie di Fibonacci un argomento affascinante e cruciale che collega il mondo della matematica pura con le applicazioni pratiche nella scienza e nella tecnologia.

I Tre Algoritmi Proposti

Possiamo implementare diversi algoritmi per generare la serie di Fibonacci in Python e confrontarli in base alle notazioni asintotiche. I principali approcci sono:

  • ricorsivo
  • iterativo
  • a programmazione dinamica.

Vediamo del codice di esempio dei tre diversi algoritmi, riportati sotto forma di 3 funzioni diverse.

Ricorsione:

def fibonacci_recursion(n):
    if n <= 1:
        return n
    else:
        return fibonacci_recursion(n-1) + fibonacci_recursion(n-2)

Iterativo:

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

Programmazione dinamica:

def fibonacci_dynamic(n):
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]

Ora possiamo confrontare le prestazioni di questi algoritmi utilizzando il tempo di esecuzione e osservando le notazioni asintotiche.

import time

def measure_time(func, *args):
    start_time = time.time()
    result = func(*args)
    end_time = time.time()
    execution_time = end_time - start_time
    return result, execution_time

n = 30 
result_recursion, time_recursion = measure_time(fibonacci_recursion, n)
result_iterative, time_iterative = measure_time(fibonacci_iterative, n)
result_dynamic, time_dynamic = measure_time(fibonacci_dynamic, n)

print(f"Recursion: {time_recursion} sec, Result: {result_recursion}")
print(f"Iterative: {time_iterative} sec, Result: {result_iterative}")
print(f"Dynamic: {time_dynamic} sec, Result: {result_dynamic}")

Eseguendo si otterrà il seguente risultato:

Recursion: 0.28981590270996094 sec, Result: 832040
Iterative: 0.0 sec, Result: 832040
Dynamic: 0.0 sec, Result: 832040

Vediamolo meglio da un punto di vista grafico. Riscrivendo il codice nella forma seguente:

import time
import matplotlib.pyplot as plt

def fibonacci_recursion(n):
    if n <= 1:
        return n
    else:
        return fibonacci_recursion(n-1) + fibonacci_recursion(n-2)

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

def fibonacci_dynamic(n):
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]

def measure_time(func, *args):
    start_time = time.time()
    result = func(*args)
    end_time = time.time()
    execution_time = end_time - start_time
    return result, execution_time

def plot_fibonacci_time_complexities(max_n):
    n_values = list(range(2, max_n + 1))
    times_recursion = []
    times_iterative = []
    times_dynamic = []

    for n in n_values:
        _, time_recursion = measure_time(fibonacci_recursion, n)
        _, time_iterative = measure_time(fibonacci_iterative, n)
        _, time_dynamic = measure_time(fibonacci_dynamic, n)

        times_recursion.append(time_recursion)
        times_iterative.append(time_iterative)
        times_dynamic.append(time_dynamic)

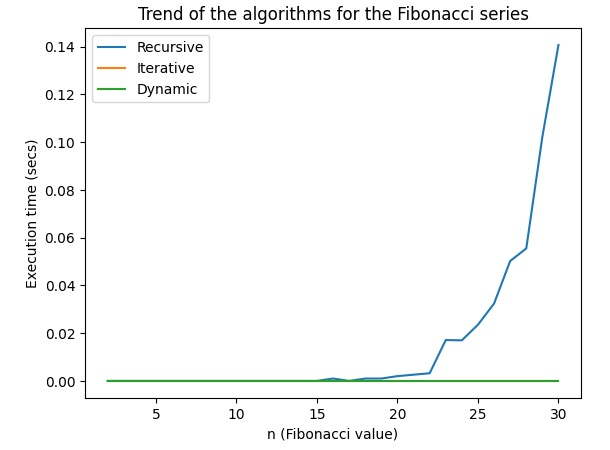
    plt.plot(n_values, times_recursion, label='Recursive')
    plt.plot(n_values, times_iterative, label='Iterative')
    plt.plot(n_values, times_dynamic, label='Dynamic')

    plt.xlabel('n (Fibonacci value)')
    plt.ylabel('Execution time (secs)')
    plt.title('Trend of the algorithms for the Fibonacci series')
    plt.legend()
    plt.show()

# Specificare il valore massimo di n per il grafico
max_n = 30
plot_fibonacci_time_complexities(max_n)
Fibonacci algorithms 01

È importante notare che l’approccio ricorsivo diventa rapidamente inefficiente per valori di n più grandi a causa della sua complessità esponenziale. La programmazione dinamica è generalmente più efficiente in termini di tempo rispetto all’approccio iterativo o ricorsivo, specialmente per input grandi, grazie alla sua complessità lineare.

Confronto Pratico tra iterazione e programmazione dinamica

Nell’esempio precedente abbiamo visto come l’algoritmo di ricorsione diventa rapidamente inefficiente. Ma per quanto riguarda gli altri due algoritmi risulta difficile poter fare delle valutazioni, dato che i tempi di esecuzioni risultano pari a 0 (troppo veloci) e gli andamenti completamente piatti. La differenza tra l’approccio iterativo e quello di programmazione dinamica può essere più evidente per valori più grandi di n. Inoltre, potremmo utilizzare la libreria timeit per ottenere misure più accurate del tempo di esecuzione. Ecco una versione aggiornata del codice:

import timeit
import matplotlib.pyplot as plt

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

def fibonacci_dynamic(n):
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]

def measure_time(func, *args):
    return timeit.timeit(lambda: func(*args), number=1000)

def plot_fibonacci_time_complexities(max_n):
    n_values = list(range(2, max_n + 1))
    times_iterative = []
    times_dynamic = []

    for n in n_values:
        time_iterative = measure_time(fibonacci_iterative, n)
        time_dynamic = measure_time(fibonacci_dynamic, n)

        times_iterative.append(time_iterative)
        times_dynamic.append(time_dynamic)

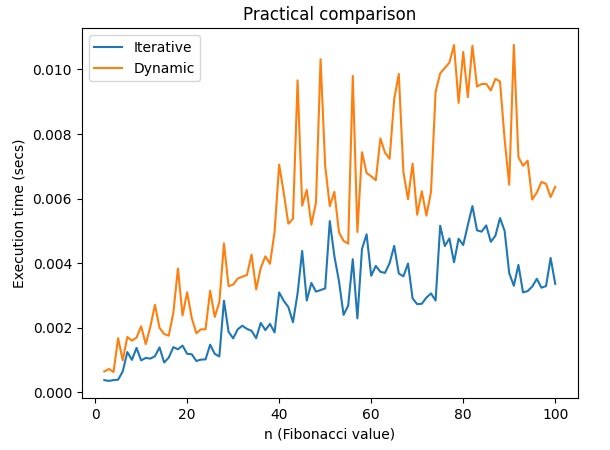
    plt.plot(n_values, times_iterative, label='Iterative')
    plt.plot(n_values, times_dynamic, label='Dynamic')

    plt.xlabel('n (Fibonacci value)')
    plt.ylabel('Tempo di esecuzione (secondi)')
    plt.title('Practical comparison')
    plt.legend()
    plt.show()

max_n = 100
plot_fibonacci_time_complexities(max_n)
Fibonacci algorithms 02

Questo codice utilizza timeit per ottenere il tempo medio di esecuzione per 1000 esecuzioni di ciascun algoritmo. Puoi notare la differenza nei tempi di esecuzione per l’approccio iterativo e quello di programmazione dinamica quando n è abbastanza grande. Se il problema persiste, potrebbe dipendere dalle specificità del tuo ambiente di esecuzione.

Considerazioni Finali

Vediamo quali sono le complessità asintotiche (O grande) per gli algoritmi proposti:

Ricorsivo:

  • Complessità temporale: O(2^n)
  • La complessità cresce in modo esponenziale con il valore di n.

Iterativo:

  • Complessità temporale: O(n)
  • La complessità temporale è lineare rispetto al valore di n, rendendo l’approccio iterativo più efficiente rispetto a quello ricorsivo.

Programmazione dinamica:

  • Complessità temporale: O(n)
  • La programmazione dinamica sfrutta la memorizzazione dei risultati intermedi per evitare di ricalcolare le stesse sottoproblemi, ottenendo così una complessità lineare rispetto al valore di n.

Quindi, in termini di efficienza asintotica, nell’esempio specifico fornito, sembra che l’approccio iterativo stia eseguendo più rapidamente rispetto all’approccio di programmazione dinamica. Questo può essere dovuto a variabili come l’implementazione specifica, l’ambiente di esecuzione e la potenza del computer.

La complessità O(n) dell’approccio iterativo e dell’approccio di programmazione dinamica indica che entrambi dovrebbero avere un andamento lineare con il crescere di n. Tuttavia, fattori come le operazioni di basso livello, la gestione della memoria e le ottimizzazioni del compilatore possono influenzare le prestazioni pratiche.

Se vuoi esaminare più approfonditamente le differenze tra i due approcci per i tuoi specifici dati di input e ambiente di esecuzione, potresti voler fare ulteriori esperimenti con valori di n più grandi o su un sistema diverso. In ogni caso, la complessità asintotica rimane uno strumento teorico utile per valutare il comportamento degli algoritmi su input sufficientemente grandi.

Conclusioni

In conclusione, la scelta dell’algoritmo giusto è fondamentale per ottenere prestazioni ottimali in base alle specifiche esigenze del problema. Nel contesto della serie di Fibonacci, abbiamo esaminato tre approcci principali: ricorsivo, iterativo e di programmazione dinamica. Ognuno di questi ha le proprie caratteristiche e complessità temporali.

Il confronto tra l’approccio iterativo e quello di programmazione dinamica ha dimostrato che, nonostante le complessità asintotiche siano entrambe O(n), le prestazioni pratiche possono variare a seconda delle circostanze. In alcuni casi, l’approccio iterativo potrebbe eseguirsi più velocemente, mentre in altri casi, la programmazione dinamica può mostrare maggiore efficienza grazie alla memorizzazione delle soluzioni intermedie.

È importante sottolineare che la scelta dell’algoritmo ottimale dipende da diversi fattori, tra cui la dimensione del problema, la complessità dell’implementazione, le risorse disponibili e le peculiarità dell’input. Invito pertanto alla sperimentazione e all’esplorazione di soluzioni ottimizzate, poiché ogni contesto può richiedere un approccio diverso.

La pratica e l’esplorazione attiva delle diverse opzioni sono fondamentali per capire appieno le prestazioni degli algoritmi in uno specifico contesto. L’analisi delle complessità asintotiche fornisce una guida teorica, ma l’esperienza pratica e la comprensione del problema sono cruciali per prendere decisioni informate nella scelta degli algoritmi.

Lascia un commento