La cinematica inversa (Inverse Kinematics)

Post Views: 10.802

La cinematica inversa (Inverse Kinematics)

Per cinematica inversa si intende l’insieme di metodologie che permettono di determinare il moto di un robot per raggiungere una posizione desiderata.

Ma non c’è modo migliore di spiegare bene cosa sia la cinematica inversa se non con un esempio pratico…

Il manipolatore a 2 link e a 2 giunti

Prendiamo in considerazione il modello più semplice di robot.

Supponiamo di avere un manipolatore composto da due link e due giunti piegati negli angoli $\theta_1^A$ e $\theta_2^A$ , rispettivamente. L’estremità efficace si troverà in una posizione A definita dalle coordinate $(x_A, y_A)$ . Questa è la posizione di partenza.

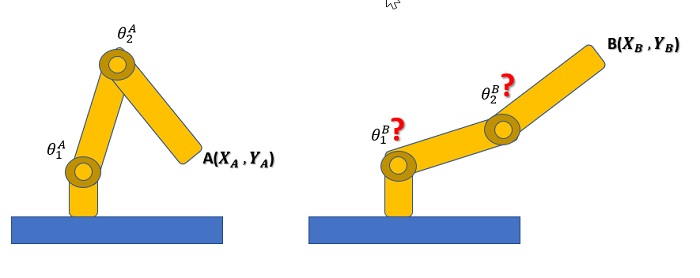
Inverse kinematics - la cinematica inversa

Ora però l’estremità efficace per lavorare dovrà muoversi in una nuova posizione B avente coordinate $(x_B, y_B)$ . Quali saranno i due nuovi angoli $\theta_1^B$ e $\theta_2^B$ che i due giunti dovranno assumere per fare in modo che l’estremità efficace si trovi correttamente nella posizione B?

Questo è un classico problema di cinematica inversa ( Inverse kinematics).

Come risolvere?

Per poter risolvere tale problema sarà necessario utilizzare le equazioni di cinematica diretta del manipolatore. Dato che queste equazioni non sono lineari, il trovare una soluzione non è certamente un impresa così facile e diretta. Inoltre, spesso la soluzione non è unica. Infatti si potranno avere diverse combinazioni di angoli dei giunti per ottenere la stessa posizione (x,y) desiderata. Questi aspetti aumentano maggiore è la complessità del sistema manipolatore in studio.

Anche il caso più semplice, cioè il caso che abiamo preso in considerazione, quello di un manipolatore a due link e due giunti, presenta alcune difficoltà.

non tutte le posizioni (x,y) sono raggiungibili dall’estremità efficace ed in questo caso non ci sono soluzioni nelle equazioni.
ci possono essere due soluzioni, corrispodenti a due configurazioni diverse del manipolatore (elbow up e elbow down).

Inverse kinematics - configurazioni di un manipolatore a 2 link elbow up e elbow down

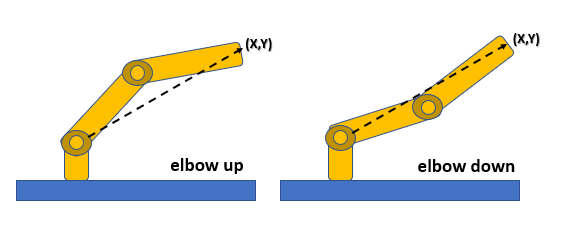
Risolviamo analiticamente il problema considerando il seguente diagramma:

Inverse kinematics - parametri del manipolatore

Si può utilizzare la legge dei coseni per ricavare l’angolo θ₂

$cos \theta_2 = \frac { x^2 + y^2 - \alpha_1^2 - \alpha_2^2 }{ 2 \alpha_1 \alpha_2 } = D$

$\theta_2 = cos^{-1} (D)$

Un modo più semplice sarà quello di considerare invece sin(θ₂).

$sin \theta_2 = \pm \sqrt{ 1 - D^2 }$

E quindi, si può ricavare θ₂ come

$\theta_2 = tan^{-1} \frac{\pm \sqrt{ 1 - D^2}}{D}$

Con questo tipo di approccio analitico è possibile considerare entrambe le soluzioni (configurazioni elbow-up ed elbow-down) scegliendo i segni positivo e negativo nell’equazione.

$\theta_1 = tan^{-1} (\frac{y}{x}) - tan^{-1} (\frac{\alpha_2 sin \theta_2}{\alpha_1 + \alpha_2 cos \theta_2})$

Come si vede dall’equazione sopra, si deduce che l’angolo θ₁ dipende da θ₂. Questa valutazione è plausibile dato che quest’angolo dipenderà assolutamente da quale soluzione verrà scelta per θ₂.

La cinematica inversa per casi più complessi

Quindi i problemi di cinematica inversa si basano sulla determinazione di un insieme di possibili configurazioni dei giunti che permettono di far raggiungere l’estremità efficace nel punto desiderato.

Dal punto di vista applicativo sono state create numerose tecniche e metodi, che fanno uso principalmente di algoritmi con alla base dei calcoli numerici da eseguire su di un calcolatore. Nonostante questo, ancora oggi tali metodi soffrono di un costo computazionale ancora altro, e spesso si ottengono risultati non sempre realistici.

Nei prossimi articoli illustreremo qualche caso applicativo e alcnune di queste tecniche di calcolo.