I Decision Trees come modello di apprendimento nel Machine Learning

Un Decision Tree (albero decisionale) è un modello di apprendimento automatico che rappresenta una serie di decisioni logiche prese in base ai valori dei attributi. È una struttura ad albero che viene utilizzata per prendere decisioni o fare previsioni a partire dai dati di input.

[wpda_org_chart tree_id=18 theme_id=50]

I Decision Trees (Alberi Decisionali)

Un albero decisionale è costituito da nodi e rami. I nodi rappresentano decisioni o test su un attributo, mentre i rami rappresentano le possibili conseguenze di una decisione o un test. Gli alberi decisionali sono utilizzati sia per problemi di classificazione che di regressione.

Ecco come funziona il processo di creazione di un Decision Tree:

1. Selezione dell’attributo: L’algoritmo di creazione dell’albero decisionale sceglie l’attributo migliore da utilizzare come nodo radice. Questa scelta viene fatta in base a criteri come l’entropia, il guadagno di informazione o il Gini impurity. L’attributo scelto viene utilizzato per suddividere il set di dati in sottoinsiemi più piccoli.
2. Suddivisione dei dati: I dati vengono suddivisi in base ai valori dell’attributo scelto. Ogni valore dell’attributo genera un ramo nell’albero, e i dati vengono assegnati ai rami corrispondenti.
3. Ripetizione: Il processo di selezione dell’attributo e suddivisione dei dati viene ripetuto per ciascun sottoinsieme di dati in ogni nodo interno. Questo processo continua fino a quando non viene raggiunto un criterio di arresto, come ad esempio una profondità massima dell’albero o un numero minimo di campioni in un nodo.
4. Nodi foglia: Una volta che il processo di suddivisione raggiunge i nodi foglia, cioè i nodi finali dell’albero, vengono assegnate etichette di classificazione (nel caso di un problema di classificazione) o valori di previsione (nel caso di un problema di regressione).

I vantaggi degli alberi decisionali includono la facilità di interpretazione, poiché le decisioni sono rappresentate in modo intuitivo come flussi logici, e la capacità di gestire dati sia numerici che categorici. Tuttavia, gli alberi decisionali possono essere inclini all’overfitting, specialmente quando sono profondi e complessi.

Gli alberi decisionali possono essere ulteriormente migliorati utilizzando tecniche come la potatura (pruning), che riduce la complessità dell’albero per migliorare la generalizzazione, e l’ensemble learning, in cui più alberi decisionali vengono combinati per formare modelli più forti, come:

• Random Forest
• Gradient Boosting.

ARTICOLO DI APPROFONDIMENTO

Random Forest

ARTICOLO DI APPROFONDIMENTO

Gradient Boosting

Esistono anche ulteriori modelli algoritmici più complessi specializzati per i Decision Tree come:

• CART

ARTICOLO DI APPROFONDIMENTO

CART

Un po’ di storia

Gli alberi decisionali hanno una storia lunga e interessante nel campo del machine learning e dell’intelligenza artificiale. La loro evoluzione ha portato a sviluppare tecniche più avanzate, come Random Forests e Gradient Boosting. Ecco una panoramica della storia dei decision trees nel machine learning:

Anni ’60: L’idea alla base degli alberi decisionali ha radici negli anni ’60. Il concetto di “programmi di decisione” è stato introdotto da Hunt, Marin e Stone nel 1966. L’obiettivo era creare algoritmi che potessero apprendere come prendere decisioni attraverso regole logiche basate sui dati.

Anni ’70: Negli anni ’70, il concetto di alberi decisionali è stato ulteriormente sviluppato da Michie e Chambers. Hanno introdotto l’idea di creare alberi di decisione che potessero essere utilizzati per prendere decisioni su problemi di classificazione.

Anni ’80: Negli anni ’80, il concetto di alberi decisionali ha continuato a evolversi con l’introduzione di nuove tecniche di apprendimento automatico. ID3 (Iterative Dichotomiser 3), sviluppato da Ross Quinlan nel 1986, è uno dei primi algoritmi di apprendimento automatico basati sugli alberi decisionali. ID3 utilizzava il concetto di guadagno di informazione per selezionare gli attributi migliori per la suddivisione.

Anni ’90: Negli anni ’90, l’approccio agli alberi decisionali è stato ulteriormente migliorato con l’introduzione di nuovi algoritmi e tecniche. C4.5, introdotto da Ross Quinlan nel 1993, ha migliorato e esteso ID3, consentendo di gestire attributi numerici e mancanti e introducendo la potatura (pruning) degli alberi per migliorare la generalizzazione.

Anni 2000 e oltre: Negli anni 2000, l’interesse per gli alberi decisionali è cresciuto ulteriormente. Sono stati sviluppati algoritmi come CART (Classification and Regression Trees), che può essere utilizzato sia per problemi di classificazione che di regressione. Inoltre, sono state introdotte tecniche di ensemble learning basate su alberi decisionali, come Random Forests (2001) di Leo Breiman e Gradient Boosting (2001) di Jerome Friedman.

Oggi, gli alberi decisionali e le loro varianti sono ampiamente utilizzati nell’apprendimento automatico e nel data science. Sono apprezzati per la loro facilità di interpretazione, la capacità di gestire dati eterogenei e la capacità di gestire sia problemi di classificazione che di regressione. Gli alberi decisionali sono spesso combinati in ensemble methods come Random Forests e Gradient Boosting per migliorare ulteriormente le prestazioni dei modelli.

Usare i Decision Trees con scikit-learn

I Decision Trees possono essere usati per due problemi di Machine Learning:

• Classificazione
• Regressione

In Python, puoi utilizzare la libreria scikit-learn per creare e addestrare alberi decisionali utilizzando le classi DecisionTreeClassifier per la classificazione e DecisionTreeRegressor per la regressione.

La Classificazione con i Decision Tree con scikit-learn

Ecco un esempio di come puoi utilizzare scikit-learn per creare e addestrare un Decision Tree Classifier utilizzando il dataset Breast Cancer Wisconsin.

Step 1: Importa le librerie necessarie

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

In questa sezione, stiamo importando le librerie necessarie per creare e addestrare il Decision Tree Classifier.

Step 2: Carica il dataset e dividi i dati

# Carica il dataset Breast Cancer Wisconsin come esempio
breast_cancer = load_breast_cancer()
X = breast_cancer.data
y = breast_cancer.target

# Dividi il dataset in set di addestramento e di test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Qui stiamo caricando il dataset Breast Cancer Wisconsin utilizzando la funzione load_breast_cancer() e dividendo i dati in set di addestramento e di test utilizzando la funzione train_test_split().

Step 3: Crea e addestra il classificatore Decision Tree

# Crea il classificatore Decision Tree
clf = DecisionTreeClassifier(random_state=42)

# Addestra il classificatore sul set di addestramento
clf.fit(X_train, y_train)

In questo step, stiamo creando un oggetto DecisionTreeClassifier e lo addestriamo sul set di addestramento utilizzando il metodo fit().

Step 4: Effettua previsioni e calcola l’accuratezza

# Effettua previsioni sul set di test
predictions = clf.predict(X_test)

# Calcola l'accuratezza delle previsioni
accuracy = accuracy_score(y_test, predictions)
print("Accuracy:", accuracy)

In questo passaggio, stiamo effettuando previsioni sul set di test utilizzando il metodo predict() del classificatore addestrato e quindi calcoliamo l’accuratezza delle previsioni utilizzando la funzione accuracy_score().

Eseguendo si ottiene:

Accuracy: 0.9473684210526315

Adesso possiamo valutare l’idea di aggiungere alcune visualizzazioni utili per comprendere la validità o meno del modello che abbiamo appena utilizzato. Per prima cosa analizziamo la matrice di confusione.

from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt

cm = confusion_matrix(y_test, predictions)
sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['Benigno', 'Maligno'], yticklabels=['Benigno', 'Maligno'])
plt.xlabel('Predizioni')
plt.ylabel('Valori Veri')
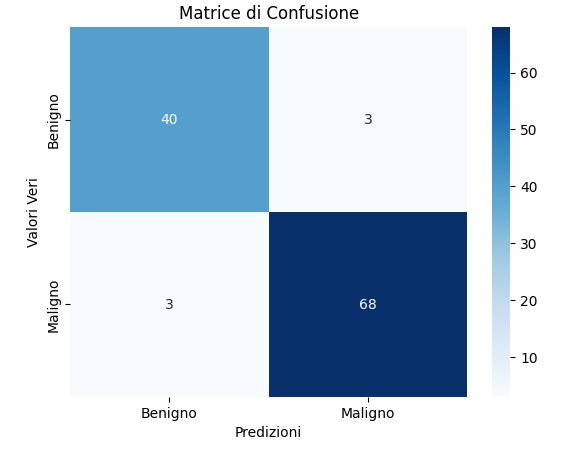
plt.title('Matrice di Confusione')
plt.show()

Eseguendo si ottiene una matrice di confusione, Questo grafico visualizza il numero di veri positivi, falsi positivi, veri negativi e falsi negativi, offrendo una panoramica più dettagliata delle prestazioni del tuo modello.

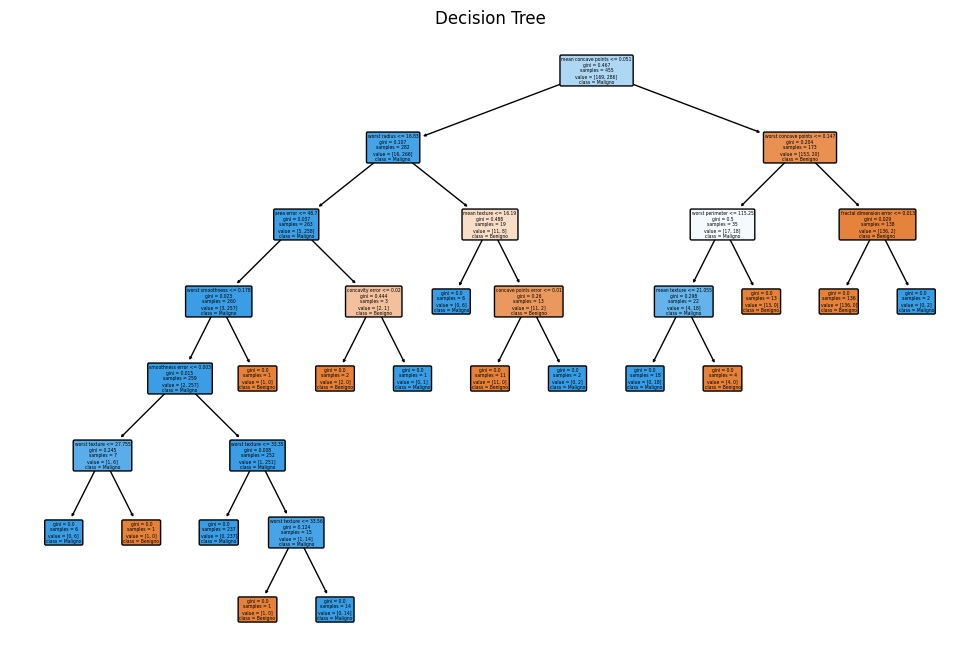
Adesso, il prossimo grafico avrà lo scopo di visualizzare la struttura dell’albero decisionale.

from sklearn.tree import plot_tree

plt.figure(figsize=(12, 8))
plot_tree(clf, filled=True, feature_names=breast_cancer.feature_names, class_names=['Benigno', 'Maligno'], rounded=True)
plt.title('Decision Tree')
plt.show()

Eseguendo il codice si ottiene il grafico seguente in cui viene rappresentato l’intero albero decisionale, aiutandoti a comprendere le decisioni prese dal modello. Può essere particolarmente utile se l’albero non è troppo grande.

Andiamo avanti con le nostre visualizzazioni del modello di Albero decisionale. Questa volta utilizzeremo una curva ROC.

from sklearn.metrics import roc_curve, auc

probas = clf.predict_proba(X_test)[:, 1]
fpr, tpr, thresholds = roc_curve(y_test, probas)
roc_auc = auc(fpr, tpr)

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (AUC = {:.2f})'.format(roc_auc))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
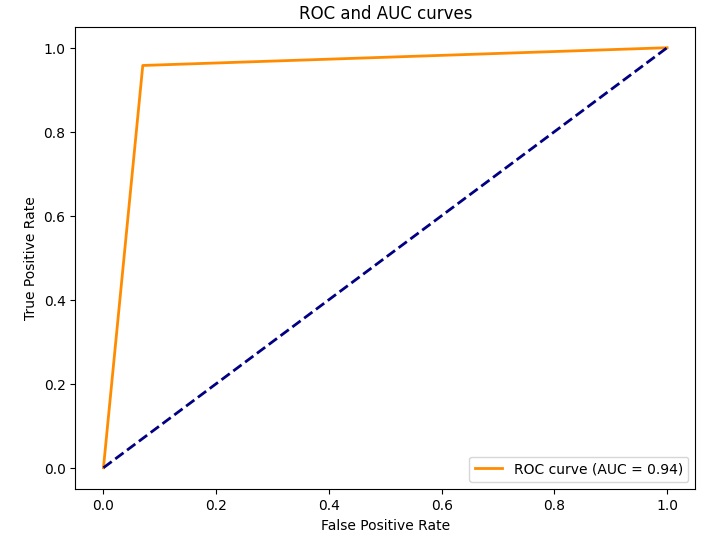
plt.title('ROC and AUC curves')
plt.legend(loc='lower right')
plt.show()

Eseguendo il codice si ottiene il chart della curva ROC del modello utilizzato.Questa curva ROC visualizza la trade-off tra tasso di falsi positivi e tasso di veri positivi, e l’area sotto la curva (AUC) misura la performance complessiva del modello.

Infine possiamo analizzare l’importanza delle feature per stabilire come queste giochino individualmente nella validità del modello utilizzato.

feature_importances = clf.feature_importances_
plt.barh(range(len(feature_importances)), feature_importances, align='center')
plt.yticks(range(len(breast_cancer.feature_names)), breast_cancer.feature_names)
plt.xlabel('Importance of Features')
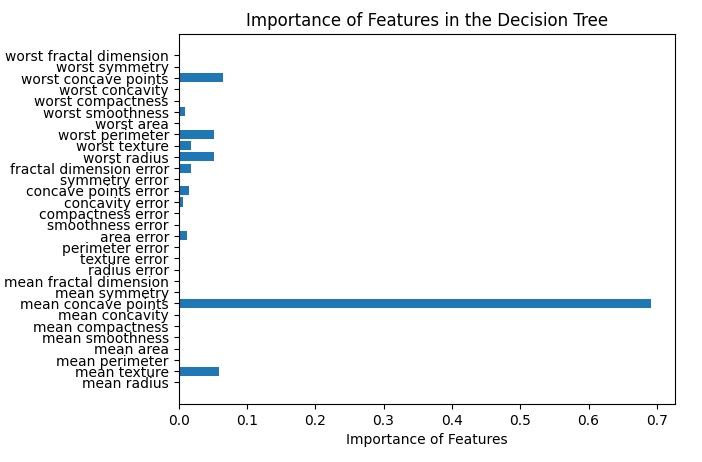
plt.title('Importance of Features in the Decision Tree')
plt.show()

Eseguendo questo snippet di codice si ottiene il diagramma a barre dove vi è raffigurato il peso di ciascuna feature nell’istruzione del modello.

Questi step combinati formano un esempio completo di come utilizzare scikit-learn per creare e addestrare un Decision Tree Classifier per un problema di classificazione. Puoi personalizzare ulteriormente il modello utilizzando gli iperparametri del Decision Tree Classifier per adattarlo alle tue esigenze.

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

La Regressione con i Decision Tree con scikit-learn

Ecco un esempio di come puoi utilizzare scikit-learn per creare e addestrare un Decision Tree Regressor utilizzando il dataset Boston Housing:

Step 1: Importa le librerie necessarie

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error

In questa sezione, stiamo importando le librerie necessarie per creare e addestrare il Decision Tree Regressor.

Step 2: Carica il dataset e dividi i dati

# Carica il dataset California Housing come esempio
housing = fetch_california_housing()
X = housing.data
y = housing.target<code>

# Dividi il dataset in set di addestramento e di test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Qui stiamo caricando il dataset California Housing utilizzando la funzione fetch_california_housing() e dividendo i dati in set di addestramento e di test utilizzando la funzione train_test_split().

Step 3: Crea e addestra il regressore Decision Tree

# Crea il regressore Decision Tree
reg = DecisionTreeRegressor(random_state=42)

# Addestra il regressore sul set di addestramento
reg.fit(X_train, y_train)

In questo step, stiamo creando un oggetto DecisionTreeRegressor e lo addestriamo sul set di addestramento utilizzando il metodo fit().

Step 4: Effettua previsioni e calcola l’errore medio quadratico

# Effettua previsioni sul set di test
predictions = reg.predict(X_test)

# Calcola l'errore medio quadratico delle previsioni
mse = mean_squared_error(y_test, predictions)
print("Mean Squared Error:", mse)

In questo passaggio, stiamo effettuando previsioni sul set di test utilizzando il metodo predict() del regressore addestrato e quindi calcoliamo l’errore medio quadratico delle previsioni utilizzando la funzione mean_squared_error().

Eseguendo si ottiene il seguente risultato:

Mean Squared Error: 0.495235205629094

Anche in questo caso, come per il problema della classificazione, potremo utilizzare delle visualizzazioni per valutare la validità del modello utilizzato. In questo caso si useranno delle visualizzazioni diverse dato che abbiamo un problema di regressione.

import matplotlib.pyplot as plt

plt.scatter(y_test, predictions)
plt.xlabel('Actual Values')
plt.ylabel('Predictions')
plt.title('Comparison between Actual Values and Forecasts')
plt.show()

Eseguendo il codice si otterrà un grafico di dispersione che mostra la relazione tra i valori effettivi e le previsioni del modello. Idealmente, i punti dovrebbero allinearsi con la linea diagonale, indicando una buona previsione.

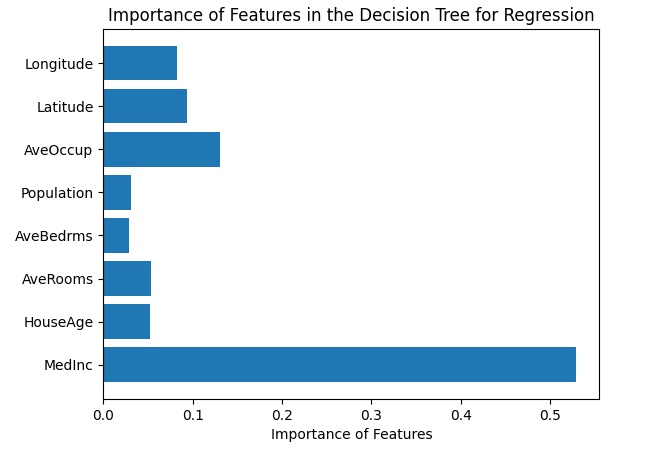
Un’altra visualizzazione è l’importanza delle feature dove viene mostrata l’importanza relativa di ciascuna feature nel processo decisionale del modello di regressione.

import numpy as np

feature_importances = reg.feature_importances_
plt.barh(range(len(feature_importances)), feature_importances, align='center')
plt.yticks(np.arange(len(housing.feature_names)), housing.feature_names)
plt.xlabel('Importance of Features')
plt.title('Importance of Features in the Decision Tree for Regression')
plt.show()

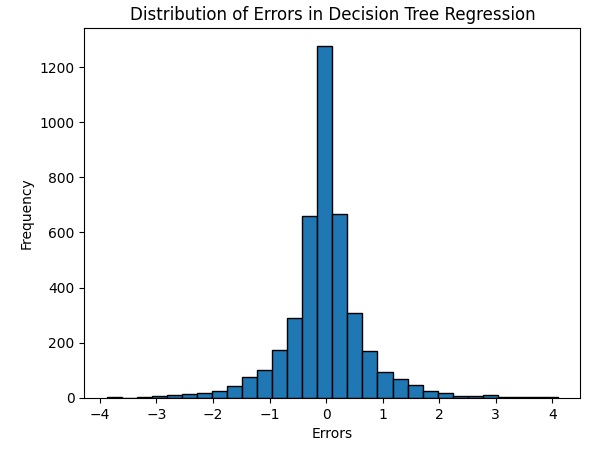
Un’altra visualizzazione è la distribuzione degli errori con un istogramma che mostra come sono distribuiti gli errori tra le previsioni del modello e i valori effettivi.

errors = y_test - predictions
plt.hist(errors, bins=30, edgecolor='black')
plt.xlabel('Errors')
plt.ylabel('Frequency')
plt.title('Distribution of Errors in Decision Tree Regression')
plt.show()

Questi step combinati formano un esempio completo di come utilizzare scikit-learn per creare e addestrare un Decision Tree Regressor per un problema di regressione. Puoi personalizzare ulteriormente il modello utilizzando gli iperparametri del Decision Tree Regressor per adattarlo alle tue esigenze.