Regression: a journey into numerical relationships and predictions

Post Views: 226

Statistical regression is a powerful tool in the data analyst’s arsenal, allowing you to explore relationships between variables and make predictions based on these relationships. In this article, we will delve deeper into regression, exploring its fundamental concepts, different types and practical applications.

Regression is a statistical technique that deals with modeling and analyzing relationships between variables. Starting from the basics of correlation, regression goes further by trying to understand how a dependent variable changes when one or more independent variables vary. This journey into the heart of numerical relationships is fundamental to making predictions and understanding the world around us.

[wpda_org_chart tree_id=9 theme_id=50]

Types of Regression: Linear, Multiple and more

Linear regression is the starting point. This model, explored by Sir Francis Galton in 1886, attempts to fit a straight line to the data. But the real world is often more complex. Multiple regression allows you to consider more than one independent variable, addressing more intricate scenarios.

Linear regression is a simple but powerful technique that attempts to model the relationship between a dependent variable and a single independent variable across a straight line. The model equation is expressed as:

$Y = \beta_0 + \beta_1X + \varepsilon$

where:

$Y$ is the dependent variable,
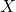$X$ is the independent variable,
$\beta_0$ is the intercept,
$\beta_1$ is the slope,
$\varepsilon$ represents the residual error.

The least squares method is commonly used to estimate the $\beta_0$ and $\beta_1$ coefficients, trying to minimize the sum of the squares of the residual errors.

When the relationship between the dependent variable and a single independent variable is not sufficient, we enter multiple regression. In this context, the model equation is extended to include multiple independent variables:

$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_kX_k + \varepsilon$

Each $\beta$ represents the contribution of the independent variables to the prediction of the dependent variable. Multiple regression offers a more complete view of complex relationships in your data, allowing you to consider the effect of multiple factors simultaneously.

Key Differences Between Linear and Multiple Regression:

Number of Variables: Linear regression involves only one independent variable, while multiple regression involves multiple independent variables.
Model Complexity: Multiple regression is more complex, allowing you to model more intricate relationships and consider the effect of multiple factors simultaneously.
Interpretation: Linear regression offers a clear interpretation of the relationship between two variables, while in multiple regression, the interpretation can be more nuanced due to interactions between variables.

In conclusion, the choice between linear and multiple regression depends on the complexity of the phenomenon studied and the specific objectives of the analysis. Linear regression is a clear starting point, while multiple regression proves crucial when relationships are inherently more intricate and involve multiple factors.

Other variations, such as polynomial regression or logistic regression, adapt to specific contexts, broadening the analyst’s arsenal. There are other even more complex forms of regression. All these types of regression are explored in depth in the Advanced Regression section.

How Linear Regression Works: The Mathematician Behind the Scenes

Regression is steeped in mathematics, with its operation based on the fundamental principle of least squares. This method tries to find the model coefficients that minimize the sum of the squares of the residual errors, i.e. the differences between the values predicted by the model and those actually observed. Let’s explore the mathematical heart behind this process:

$Y = \beta_0 + \beta_1X + \varepsilon$

Minimization of the Sum of Squares of Residual Errors:

The goal is to find the optimal values of (\beta_0) and (\beta_1) that minimize the sum of squares of the residual errors. In mathematical form, this sum is expressed as:

$\text{Min}\left(\sum_{i=1}^{n} \varepsilon_i^2\right)$

Where $n$ is the total number of observations in our dataset. The approach used to minimize this sum is known as the Least Squares Method.

Calculation of Optimal Coefficients:

To find the optimal coefficients, we derive the sum of the squared errors with respect to $\beta_0$ and [/latex]\beta_1[/latex] and force the derivatives to be equal to zero. This leads to a system of equations called “Normal Equations”. The solutions to these equations provide the optimal values of $\beta_0$ and $\beta_1$ .

The Normal Equations are given by

$\sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i) = 0$
$\sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i)X_i = 0$

Their resolution provides the following optimal values:

$\beta_1 = \frac{n(\sum_{i=1}^{n} X_iY_i) - (\sum_{i=1}^{n} X_i)(\sum_{i=1}^{n} Y_i)}{n(\sum_{i=1}^{n} X_i^2) - (\sum_{i=1}^{n} X_i)^2}$

$\beta_0 = \frac{\sum_{i=1}^{n} Y_i - \beta_1(\sum_{i=1}^{n} X_i)}{n}$

Construction of the Regression Line:

With the optimal coefficients in hand, we can construct the regression line in the Cartesian plane, representing our predictive relationship between $X$ and $Y$ .

This mathematical methodology provides a solid foundation for predictive analytics and modeling relationships in data.

Let’s calculate linear regression with Python

Here is an example Python code that implements linear regression using the Least Squares Method. We will use the numpy library for mathematical operations and matplotlib for data visualization.

import numpy as np
import matplotlib.pyplot as plt

def linear_regression(X, Y):
    # Calculation of optimal coefficients
    n = len(X)
    beta_1 = (n * np.sum(X*Y) - np.sum(X) * np.sum(Y)) / (n * np.sum(X**2) - (np.sum(X))**2)
    beta_0 = (np.sum(Y) - beta_1 * np.sum(X)) / n

    return beta_0, beta_1

def regression_line(beta_0, beta_1, X):
    return beta_0 + beta_1 * X

# Example data
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 3, 4, 2, 5])

# Calculation of optimal coefficients
beta_0, beta_1 = linear_regression(X, Y)

# Construction of the regression line
regression_line = regression_line(beta_0, beta_1, X)

# Visualization of data and regression line
plt.scatter(X, Y, label='Observed data')
plt.plot(X, regression_line, color='red', label='Regression line')
plt.xlabel('Independent Variable (X)')
plt.ylabel('Dependent Variable (Y)')
plt.legend()
plt.show()

# Printing of coefficients
print(f"Interception Coefficient (beta_0): {beta_0}")
print(f"Angular Coefficient (beta_1): {beta_1}")

Spiegazione del Codice:

La funzione regressione_lineare calcola i coefficienti ottimali (\beta_0) e (\beta_1) utilizzando il Metodo dei Minimi Quadrati.
La funzione retta_di_regressione restituisce i valori predetti della variabile dipendente utilizzando i coefficienti ottenuti.
I dati di esempio sono forniti come array numpy X e Y.
La retta di regressione viene visualizzata insieme ai dati usando matplotlib.
I coefficienti ottimali vengono stampati a schermo.

Eseguendo il codice si ottiene il risultato seguente:

Assessing Goodness of Fit: R² and Other Indicators of Success

Measuring how well the regression model fits the data is essential. The R² index (coefficient of determination) provides a measure of the proportion of variance in the dependent variable that can be explained by the independent variables. We also explore other metrics, such as mean squared error, that provide additional insights into forecast accuracy.

Some of the most common indicators include the coefficient of determination $R^2$ , the root mean square error (RMSE), and the mean absolute percentage error (MAPE).

Coefficient of Determination $R^2$ :

The coefficient $R^2$ provides a measure of the proportion of variance in the dependent variable that is explained by the model. It varies from 0 to 1, where 1 indicates perfect adaptability. The formula is:

$R^2 = 1 - \frac{\text{Somma dei quadrati degli errori residui}}{\text{Somma totale dei quadrati}}$

A value closer to 1 suggests a better fit of the model to the data.

def R2(Y, Y_pred):
    ssr = np.sum((Y - Y_pred)**2)
    sst = np.sum((Y - np.mean(Y))**2)
    r2 = 1 - (ssr / sst)
    return r2

Mean Squared Error (RMSE):

The RMSE measures the average deviation of the residuals, i.e. the differences between the predicted and observed values. A square root is applied to bring the error to the same scale as the original variables.

$RMSE = \sqrt{\frac{\sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2}{n}}$

def RMSE(Y, Y_pred):
    rmse = np.sqrt(np.mean((Y - Y_pred)**2))
    return rmse

Mean Absolute Percentage Error (MAPE):

The MAPE measures the average percentage error between predicted and observed values. It is especially useful when you want to evaluate the accuracy of your predictions in percentage terms.

$MAPE = \frac{100}{n} \sum_{i=1}^{n} \left| \frac{Y_i - \hat{Y}_i}{Y_i} \right|$

def MAPE(Y, Y_pred):
    mape = np.mean(np.abs((Y - Y_pred) / Y)) * 100
    return mape

These indicators provide a comprehensive overview of the performance of the regression model. An in-depth analysis of $R^2$ , RMSE, and MAPE helps understand the quality of the predictions and whether the model is suitable for the specific context of the data.

Let’s apply them to the previous Python example:

def R2(Y, Y_pred):
    ssr = np.sum((Y - Y_pred)**2)
    sst = np.sum((Y - np.mean(Y))**2)
    r2 = 1 - (ssr / sst)
    return r2

def RMSE(Y, Y_pred):
    rmse = np.sqrt(np.mean((Y - Y_pred)**2))
    return rmse

def MAPE(Y, Y_pred):
    mape = np.mean(np.abs((Y - Y_pred) / Y)) * 100
    return mape

r2 = R2(Y, regression_line)
rmse = RMSE(Y, regression_line)
mape = MAPE(Y, regression_line)

print(f"Coefficient of Determination (R^2): {r2}")
print(f"Mean Squared Error (RMSE): {rmse}")
print(f"Average Absolute Percentage Error (MAPE): {mape}")

Executing the following values is obtained:

Coefficient of Determination (R^2): 0.36764705882352944
Mean Squared Error (RMSE): 0.9273618495495703
Average Absolute Percentage Error (MAPE): 28.199999999999996

It can be seen that the value of the coefficient of determination is very far from the value 1. At this point some considerations can be made. From this value it certainly cannot be said that the straight line obtained with the regression method is reliable. The points from which it was obtained are too few. Or it could also be that the phenomenon we are observing does not have a linear trend.

Limitations of Regression: The Importance of Caution

While regression offers a window into understanding relationships, it is critical to consider its limitations. The assumption of linearity and the presence of hidden variables can influence the results. Additionally, the analyst must pay attention to possible misinterpretations and ethical implications of using regression models.

Absolutely, it is critical to understand the limitations of regression to use it wisely and correctly interpret the results. Here are some of the main limitations of regression:

Assumptions of the Linear Model: Linear regression is based on the assumption that the relationship between the independent variable and the dependent variable can be approximated by a straight line. In many contexts, this assumption may not be realistic, and more complex models may be necessary.
Sensitivity to Outliers: The presence of anomalous values (outliers) can significantly influence the estimate of regression coefficients, leading to distorted models. It is important to identify and manage outliers appropriately.
Multicollinearity: Multicollinearity occurs when the independent variables are highly correlated with each other. This can cause problems in estimating coefficients, making it difficult to interpret the individual contribution of each variable.
Nonlinearity of Relationship: If the relationship between variables is inherently nonlinear, linear regression may not be able to accurately model this complexity. In that case, you may need to explore nonlinear models.
Dependence on Training Data: Regression models can overfit training data, a phenomenon known as overfitting. This can lead to poor performance on new data and limit the generalization of the model.
Normally Distributed Error Assumption: Linear regression assumes that errors are normally distributed. If this assumption is not met, it could affect the reliability of confidence intervals and hypothesis tests.
Limits of Causality: Regression, by its nature, only shows correlations and does not necessarily imply causality. Identifying causal relationships requires a more in-depth approach, such as controlled experiments.
Dependence on Training Data: Regression models can overfit training data, a phenomenon known as overfitting. This can lead to poor performance on new data and limit the generalization of the model.

To mitigate these limitations, it is important to perform thorough data analysis, consider more advanced approaches when necessary, and carefully evaluate the applicability of the model to specific contexts. Regression is a powerful tool, but it must be used with awareness of its limitations and the conditions under which it is most appropriate.

Conclusion

Ultimately, regression is a beacon into the complexities of data, allowing analysts to uncover relationships and make informed predictions. This journey into the world of regression offers just a glimpse of its potential, inviting data explorers to continue discovering new avenues and applications in this vast numerical landscape.