Marginal probability - Meccanismo Complesso

Post Views: 351

Marginal probability is a probability measure that is obtained by adding (or integrating, in the case of continuous variables) the joint probability over one or more events. In other words, it involves obtaining the probability of an individual event while ignoring information about the other events involved. This operation can be performed on both discrete variables and continuous variables.

[wpda_org_chart tree_id=9 theme_id=50]

The Marginal Probability of discrete variables

To better illustrate the concept of marginal probability, let’s consider two discrete variables X and Y with their joint probability distributions $P(X, Y)$ . The marginal probability of

$P(X) = \sum_{y} P(X, Y=y)$

Similarly, the marginal probability of Y, denoted as $P(Y)$ , is obtained by summing the joint probability over all possible realizations of X:

$P(Y) = \sum_{x} P(X=x, Y)$

However, if X and Y are continuous variables, the sums are replaced by integrals in the formulas.

Marginal probability is useful because it provides information about the probability of individual events without considering the other events involved. This can be particularly important in contexts where you want to analyze or interpret probability distributions in more detail.

In short, marginal probability concerns the probability of a single event, obtained by ignoring information about other events.

Example in Python of Calculating the Marginal Probability of discrete variables

Suppose we have a two-dimensional random variable with a joint probability distribution. Below, I show an example of calculating marginal probability in Python for discrete variables:

# Example of joint probability distribution P(X, Y)
joint_prob = {
    (1, 'A'): 0.1,
    (1, 'B'): 0.2,
    (2, 'A'): 0.3,
    (2, 'B'): 0.4,
}

# Calculate the marginal probability of X
def prob_marginal_X(x):
    return sum(joint_prob[(x, y)] for y in set(y for _, y in joint_prob))

# Calculate the marginal probability of Y
def prob_marginal_Y(y):
    return sum(joint_prob[(x, y)] for x in set(x for x, _ in joint_prob))

# Function testing
x_value = 1
y_value = 'A'

prob_X = prob_marginal_X(x_value)
prob_Y = prob_marginal_Y(y_value)

print(f"Marginal probability of X={x_value}: {prob_X}")
print(f"Marginal probability of Y={y_value}: {prob_Y}")

In this example, joint_prob represents a joint probability distribution for two variables, X and Y. The functions marginal_prob_X and marginal_prob_Y calculate the marginal probabilities of X and Y, respectively.

Running the code you get:

Marginal probability of X=1: 0.30000000000000004
Marginal probability of Y=A: 0.4

Marginal probability for continuous variables

Suppose we have two continuous variables, say X and Y, and a joint density function $f(x, y)$ . The marginal probability of a single variable, say X, is the probability of observing events related only to X, regardless of the realizations of Y.

The marginal probability of X is obtained by integrating the joint density function with respect to the variable Y. Mathematically, the marginal probability of compared to Y

$f_X(x) = \int_{-\infty}^{\infty} f(x, y) \,dy$

Similarly, the marginal probability of Y (often denoted as $f_Y(y)$ is obtained by integrating the joint density function with respect to:

$f_Y(y) = \int_{-\infty}^{\infty} f(x, y) \,dx$

These marginal probabilities provide information about the distribution of each variable individually, ignoring information about the second variable. They are useful when you want to understand the distribution of one variable at a time.

Remember that in general, calculating these marginal probabilities may involve the use of integration and may require some specific techniques depending on the shape of the joint density function

Calculating Marginal Probability for Continuous Variables in Python

For continuous variables, the concept remains the same, but the sum is replaced by an integral. In Python, you could use libraries like NumPy and SciPy to perform more complex calculations with continuous variables. SciPy also provides numerical integration functions.

Suppose we have a joint density function (f(x, y)) and we want to calculate the marginal probabilities of (X) and (Y).

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
from mpl_toolkits.mplot3d import Axes3D

# We define the joint density function f(x, y)
def joint_density(x, y):
    return np.exp(-(x**2 + y**2) / 2) / (2 * np.pi)

# Let's calculate the marginal probability of X
def marginal_x(x):
    result, _ = integrate.quad(lambda y: joint_density(x, y), -np.inf, np.inf)
    return result

# Let's calculate the marginal probability of Y
def marginal_y(y):
    result, _ = integrate.quad(lambda x: joint_density(x, y), -np.inf, np.inf)
    return result

# Example of calculating the marginal probability for some specific values
x_value = 1.0
y_value = 0.5

marginal_x_value = marginal_x(x_value)
marginal_y_value = marginal_y(y_value)

print(f"Marginal probability of X per x = {x_value}: {marginal_x_value}")
print(f"Marginal probability of Y per y = {y_value}: {marginal_y_value}")

# Let's create a 3D graph of the joint density function
fig = plt.figure(figsize=(12, 6))

ax1 = fig.add_subplot(121, projection='3d')
x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)
Z = joint_density(X, Y)
ax1.plot_surface(X, Y, Z, cmap='viridis')
ax1.set_title('Joint probability density function')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Density')

# Let's create a marginal probability graph
ax2 = fig.add_subplot(222)
marginal_x_values = [marginal_x(x) for x in x_values]
ax2.plot(x_values, marginal_x_values)
ax2.set_title('Marginal probability of X')
ax2.set_xlabel('X')
ax2.set_ylabel('Marginal density')

ax3 = fig.add_subplot(224)
marginal_y_values = [marginal_y(y) for y in y_values]
ax3.plot(y_values, marginal_y_values)
ax3.set_title('Marginal probability of Y')
ax3.set_xlabel('Y')
ax3.set_ylabel('Marginal density')

plt.tight_layout()
plt.show()

Executing you get the following result:

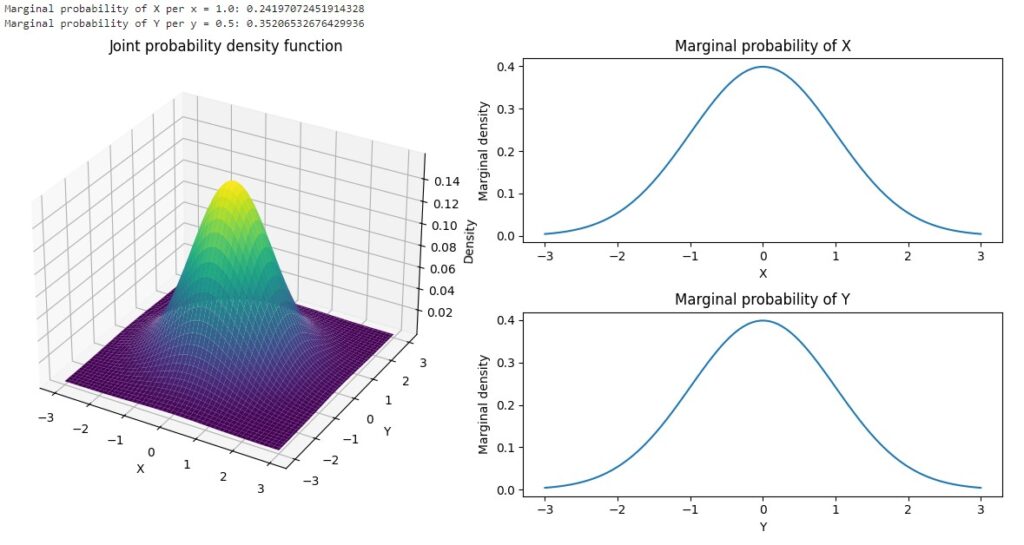
Joint density function:

The joint density function, often denoted as $f_{XY}(x, y)$ , describes the probability that the random variables $X$ and $Y$ take on specific values $x$ and $y$ . In our example, we used a two-dimensional Gaussian distribution:

$f_{XY}(x, y) = \frac{e^{-(x^2 + y^2)/2}}{2\pi}$

Marginal probability of X:

The marginal probability of $X$ , denoted as $f_X(x)$ , is obtained by integrating the joint density function with respect to $y$ over the entire domain of $y$ :

$f_X(x) = \int_{-\infty}^{\infty} f_{XY}(x, y) \,dy$

In our case, we use numerical integration to calculate this quantity:

$f_X(x) = \int_{-\infty}^{\infty} \frac{e^{-(x^2 + y^2)/2}}{2\pi} \,dy$

Marginal probability of Y:

Similarly, the marginal probability of $Y$ , denoted as $f_Y(y)$ , is obtained by integrating the joint density function with respect to $x$ over the entire domain of $x$ :

$f_Y(y) = \int_{-\infty}^{\infty} f_{XY}(x, y) \,dx$

In our case, we use numerical integration to calculate this quantity:

$f_Y(y) = \int_{-\infty}^{\infty} \frac{e^{-(x^2 + y^2)/2}}{2\pi} \,dx$

Interpretation:

The marginal probabilities of $X$ and $Y$ represent the probability distributions of each variable, ignoring the other. The plots show the shape of the joint density function in 3D space, along with plots of the marginal probabilities over $X$ and $Y$ . This provides a comprehensive view of the relationships between random variables and marginal distributions.

This example is very generic and can be adapted to model specific joint distributions of continuous variables.