
Hypothesis Testing is a fundamental tool in inferential statistics that allows you to make informed decisions based on the data collected. This methodology is widely used in various fields, from scientific research to economics, from medicine to engineering.
[wpda_org_chart tree_id=9 theme_id=50]
What is Hypothesis Testing?
In simple terms, Hypothesis Testing is a process of evaluating population claims based on data collected from a representative sample of that population. We start from two hypotheses:
- Null Hypothesis
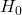 : It states that there is no relevant effect or difference. Usually, it represents the “status quo” or the absence of change.
: It states that there is no relevant effect or difference. Usually, it represents the “status quo” or the absence of change. - Alternative Hypothesis
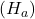 : It proposes that there is a relevant effect or difference. It can be unilateral (indicating a specific direction) or bilateral (simply indicating that there is a difference).
: It proposes that there is a relevant effect or difference. It can be unilateral (indicating a specific direction) or bilateral (simply indicating that there is a difference).
The Null Hypothesis
The null hypothesis plays a fundamental role. Often referred to as ![]() , it represents a state of “status quo” or no effect. In other words, it postulates that there are no observable differences or effects in a given context. The goal of hypothesis analysis is to evaluate whether there is sufficient evidence in the data to reject this null hypothesis in favor of an alternative hypothesis.
, it represents a state of “status quo” or no effect. In other words, it postulates that there are no observable differences or effects in a given context. The goal of hypothesis analysis is to evaluate whether there is sufficient evidence in the data to reject this null hypothesis in favor of an alternative hypothesis.
The alternative hypothesis
The alternative hypothesis, often referred to as ![]() or
or ![]() , is the statement that attempts to suggest a significant effect, difference, or change in the population. In other words, it represents the opposite of the null hypothesis. For example, if the null hypothesis states that there are no significant differences, the alternative hypothesis might state that there are actual, measurable differences.
, is the statement that attempts to suggest a significant effect, difference, or change in the population. In other words, it represents the opposite of the null hypothesis. For example, if the null hypothesis states that there are no significant differences, the alternative hypothesis might state that there are actual, measurable differences.
There are different forms of alternative hypotheses, depending on the nature of the research question. Some examples include:
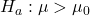 – The population average is greater than a certain value
– The population average is greater than a certain value 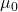 .
.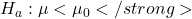 – The population average is less than a certain value
– The population average is less than a certain value 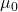 .
.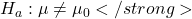 – The population mean is different from a certain value
– The population mean is different from a certain value 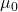 . (bidirectional).
. (bidirectional).
Where ![]() . represents the population average. These examples illustrate the alternative hypothesis for a population mean hypothesis test, but can be adapted for other types of tests.
. represents the population average. These examples illustrate the alternative hypothesis for a population mean hypothesis test, but can be adapted for other types of tests.
Hypothesis analysis involves evaluating the evidence in the data to decide whether to reject the null hypothesis in favor of the alternative hypothesis. The choice between the different forms of alternative hypotheses depends on the specificity of the research question and the nature of the relationship one wishes to test
How does it work?
The Hypothesis Testing process follows a systematic model:
- Formulation of Hypotheses: We start by clearly defining the null hypothesis and the alternative hypothesis, based on expectations and the research question.
- Data Collection: Data is collected through experiments or observations, trying to obtain a representative sample of the population of interest.
- Choice of Statistical Test: Depending on the nature of the data and the research question, the appropriate statistical test is selected. For example, the t-test can be used to compare means, while the chi-square test can be used to analyze the frequency distribution.
- Determination of the Significance Level
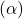 : A significance level is set, often at 0.05. This value represents the maximum acceptable probability of committing a Type I error (incorrectly rejecting the null hypothesis).
: A significance level is set, often at 0.05. This value represents the maximum acceptable probability of committing a Type I error (incorrectly rejecting the null hypothesis). - Calculation of Test Statistics: You calculate the test statistic using the collected data..
- Decision: By comparing the test statistic to the known probability distribution (under the null hypothesis), we calculate the p-value, which represents the probability of obtaining a test statistic at least as extreme as the observed one. If the p-value is lower than the significance level, the null hypothesis can be rejected.
- Interpretation: The result is interpreted in light of the hypotheses formulated. If the null hypothesis is rejected, it can be concluded that there is sufficient evidence to support the alternative hypothesis.
The Significance Level
The significance level represents the maximum acceptable probability of committing a type I error, i.e. incorrectly rejecting the null hypothesis when it is actually true. It is often indicated with the symbol (\alpha).
Commonly, the significance level value is set at 0.05 or 5%. This means that there is a 5% chance of incorrectly rejecting the null hypothesis when it is true. However, the value of (\alpha) can be chosen based on the specific needs of the study or research.
If the p-value obtained from the hypothesis test is less than the significance level (\alpha), there is sufficient evidence to reject the null hypothesis. On the other hand, if the p-value is greater than (\alpha), you do not have enough evidence to reject the null hypothesis.
It is important to note that the significance level is a subjective choice and can influence the nature of the conclusions drawn from hypothesis testing. Reducing the significance level makes the test more conservative, requiring stronger evidence to reject the null hypothesis, but increasing the risk of missing real effects (type II error). On the contrary, increasing the significance level makes the test less conservative, facilitating the detection of effects, but increasing the risk of erroneously rejecting the null hypothesis (type I error). The choice of the significance level is therefore a question of balancing these two types of errors and the practical consequences of decisions based on hypothesis testing.
Practical example of Hypothesis Testing with Python
Let’s imagine we are conducting an experiment on a new drug and we want to test whether the drug is effective in reducing blood pressure. Our hypotheses could be:
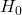 : The drug has no effect on blood pressure
: The drug has no effect on blood pressure 
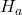 : The drug reduces blood pressure
: The drug reduces blood pressure 
After collecting the data and calculating the test statistic:
Setting the significance level value at 0.05.
- if
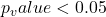 then the alternative hypothesis holds
then the alternative hypothesis holds 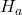 ,
, - if
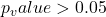 then the null hypothesis holds
then the null hypothesis holds 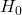 .
.
Let’s look at an example Python code that simulates an experiment with a drug and tests whether the drug has a significant effect on blood pressure. We will use the numpy library to generate random data and matplotlib to create an illustrative plot.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_1samp
# We simulate blood pressure data before and after taking the drug
np.random.seed(42) # Per rendere i risultati riproducibili
before = np.random.normal(loc=120, scale=10, size=100)
after = before - np.random.normal(loc=5, scale=2, size=100)
# Let's run the t-test
t_statistic, p_value = ttest_1samp(after - before, 0)
# We set the significance level at 0.05
alpha = 0.05
# Let's create a graph to visualize the data
plt.figure(figsize=(10, 6))
# Graph of distributions before and after the drug
plt.hist(before, bins=20, alpha=0.5, label='Prima del Farmaco')
plt.hist(after, bins=20, alpha=0.5, label='Dopo il Farmaco')
plt.title('Distribution of Blood Pressure Before and After the Drug')
plt.xlabel('Blood pressure')
plt.ylabel('Frequency')
plt.legend()
plt.show()
# We print the test result
if p_value < alpha:
print("Reject the null hypothesis. The drug has a significant effect on blood pressure.")
else:
print("Fail to reject the null hypothesis. There is not enough evidence to say that the drug has a significant effect on blood pressure.")In this example, we are simulating blood pressure data before and after taking the drug by running a left-handed t-test and graphing the distributions of the data. Finally, the hypothesis test is performed, and the result is printed along with the graph. Please remember that simulated data is for illustrative purposes only and may not reflect reality.

More Hypothesis Testing with Python
Let’s see an example of Python code that performs a two-sided t-test on the mean of a sample. In this case, we consider a sample of data and want to test whether its mean is significantly different from a reference value:
import numpy as np
from scipy.stats import ttest_1samp
# Let's generate a data sample (replace this with your real data)
data_sample = np.random.normal(loc=5, scale=2, size=30)
# We define the null hypothesis: the mean is equal to 4
null_hypothesis_mean = 4
# We define the alternative hypothesis: the mean is different from 4 (two-way)
alternative_hypothesis = "two-sided"
# Let's run the t-test
t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean)
# We set the significance level (usually 0.05)
alpha = 0.05
# We compare the p-value with the significance level
if p_value < alpha:
print("Reject the null hypothesis. There is enough evidence to suggest a significant difference.")
else:
print("Fail to reject the null hypothesis. There is not enough evidence to suggest a significant difference.")Running the code you get:
Reject the null hypothesis. There is enough evidence to suggest a significant difference.In this example, the null hypothesis ![]() states that the population mean is equal to 4, while the alternative hypothesis ((H_a)) is bidirectional, indicating that the mean is different from 4. The t test is performed, and based on the p-value compared with the significance level, we decide whether to reject the null hypothesis or not.
states that the population mean is equal to 4, while the alternative hypothesis ((H_a)) is bidirectional, indicating that the mean is different from 4. The t test is performed, and based on the p-value compared with the significance level, we decide whether to reject the null hypothesis or not.
The Critical Region
The critical region is the range of values of a test statistic that would lead to rejection of the null hypothesis during a hypothesis test. In other words, it is the set of results that are so extreme as to suggest that the null hypothesis is invalid.
The decision to reject the null hypothesis is based on the comparison between the test statistic calculated from the data and a critical threshold corresponding to the chosen significance level ((\alpha)). If the test statistic falls in the critical region, we reject the null hypothesis; otherwise, we do not reject it.
For example, in the context of a univariate t-test, the critical region might be the upper and lower tails of the t-distribution depending on the value of (\alpha) you select. If the test statistic falls in one of these tails, we reject the null hypothesis.
The choice of the critical region depends on the type of test (unilateral or bilateral) and the significance level chosen. It is a key concept in conducting and interpreting hypothesis tests, as it helps define the boundaries beyond which observations are believed to be so extreme that they are not explained simply by chance, but rather indicate a significant effect
The p-value and the q-value
The p-value and q-value are both measures used in statistics, but they serve slightly different purposes.
p-value:
The p-value, or probability value, is a measure that indicates the probability of obtaining a result as extreme or more extreme than the one observed, under the null hypothesis. In other words, the p-value gives an indication of how inconsistent your observations are with the null hypothesis. If the p-value is lower than your significance level (often 0.05), you may decide to reject the null hypothesis.
# Example of obtaining the p-value from a t-test
from scipy.stats import ttest_1samp
data_sample = [3, 4, 5, 6, 7]
null_hypothesis_mean = 4.5
t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean)
print(f"P-value: {p_value}")Running you get:
P-value: 0.5185185185185183q-value:
The q-value, or correction value for false positive rates, is often used in contexts where many tests are performed simultaneously. For example, when running multiple tests (testing many hypotheses simultaneously), the q-value helps control the rate of false positives (Type I error) by taking into account the number of tests performed. A low q-value indicates that a result is statistically significant, even after correction for multiple testing.
# Example of obtaining the q-value with FDR (False Discovery Rate) correction
from statsmodels.stats.multitest import multipletests
# List of p-values obtained from multiple tests
p_values = [0.03, 0.12, 0.04, 0.09]
# FDR Correction
reject, q_values, _, _ = multipletests(p_values, method='fdr_bh')
print(f"Q-values: {q_values}")By performing you get:
Q-values: [0.08 0.12 0.08 0.12]In summary, while the p-value is a measure of the probability that your data is compatible with the null hypothesis, the q-value is used to correct error rates when many tests are run simultaneously.
Tailed Test
A tailed test is a type of hypothesis test in which the critical region is located on only one side of the distribution of the test statistic. There are two main types of one-sided tests:
- Unilateral to the left (Left-tailed): The critical region is in the left tail of the distribution. This type of test is used when you want to test whether the test statistic is significantly lower than a certain value.
- Unilateral to the right (Right-tailed): The critical region is in the right tail of the distribution. This type of test is used when you want to test whether the test statistic is significantly higher than a certain value.
For example, consider a t-test on a one-sample mean:
- A left-tailed test could be used to test whether the sample mean is significantly less than a certain value.
- A right-tailed test could be used to test whether the sample mean is significantly above a certain value.
Here is an example of right-sided with the scipy.stats module in Python
from scipy.stats import ttest_1samp
data_sample = [3, 4, 5, 6, 7]
null_hypothesis_mean = 4.5
# Unilateral test on the right
t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean)
print(f"P-value: {p_value/2}") # We divide by 2 to get the correct p-value for the one-sided testIn the right-handed test, the p-value is divided by 2 because we are only interested in one tail of the distribution.
P-value: 0.25925925925925913One-sided tests are appropriate when there is a specific interest in detecting a change in a particular direction, for example, if we expect the test statistic to be larger or smaller than a certain reference value.
Two-Tailed Test
The two-tailed test is a type of hypothesis test in which the critical region is divided between both tails of the distribution of the test statistic. This type of test is used when you want to evaluate whether the test statistic is significantly different from a certain value, without specifying in which direction.
A common example of a two-tailed test is when you want to test whether the mean of a sample is different from a certain value. In this case, we seek to identify whether there is sufficient evidence to conclude that the sample mean is significantly higher or lower than the specified value.
Here is an example of a two-tailed test with the scipy.stats module in Python
from scipy.stats import ttest_1samp
data_sample = [3, 4, 5, 6, 7]
null_hypothesis_mean = 4.5
# Bilateral test
t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean)
print(f"P-value: {p_value}")In a two-tailed test, the p-value provided represents the probability that the test statistic is this extreme or more extreme, in both the upper and lower tails of the distribution, under the null hypothesis.
P-value: 0.5185185185185183If the p-value is less than the chosen significance level (usually 0.05), it can be concluded that there is sufficient evidence to reject the null hypothesis, indicating that the test statistic is significantly different from the specified value.
Conclusions
Hypothesis Testing provides a methodological framework for making decisions based on data, introducing scientific rigor into statistical analyses. Its correct application contributes to the validity and robustness of the conclusions drawn from the research, ensuring that the claims made are supported by solid evidence.
