Analisi di Algoritmi: la notazione asintotica e la dimensione di un problema

Post Views: 234

La dimensione di un problema e la notazione asintotica header

Nel vasto universo dell’informatica, la progettazione e l’analisi degli algoritmi giocano un ruolo cruciale nell’ottimizzazione delle soluzioni ai problemi computazionali. Per comprendere appieno l’efficienza e le prestazioni di un algoritmo, è essenziale saper valutare come il suo comportamento varia in relazione alle dimensioni del problema in input. Esploreremo due concetti fondamentali per l’analisi degli algoritmi: la notazione asintotica e la dimensione di un problema. Questi strumenti ci consentiranno di affrontare le sfide legate alle prestazioni degli algoritmi in modo chiaro e conciso.

[wpda_org_chart tree_id=42 theme_id=50]

Dimensione di un Problema

La dimensione di un problema negli algoritmi si riferisce alla quantità di risorse richieste da un algoritmo in relazione alle dimensioni dell’input. Comprendere come la dimensione del problema influisce sulle prestazioni degli algoritmi è fondamentale per valutare l’efficienza delle soluzioni proposte.

Esempio con Ordinamento:
- Supponiamo di avere un algoritmo di ordinamento. La dimensione del problema in questo caso potrebbe essere la lunghezza dell’array da ordinare. Se l’array ha n elementi, la dimensione del problema è n.
Influenza sulle Prestazioni:
- La dimensione del problema è spesso correlata al tempo di esecuzione e alla complessità dell’algoritmo. Ad esempio, un algoritmo che ordina un piccolo array può essere efficiente, ma potrebbe diventare impraticabile quando si tratta di un array molto grande.
Analisi della Crescita:
- Studiare come il tempo di esecuzione di un algoritmo cresce in relazione alla dimensione del problema è essenziale. Gli algoritmi che mantengono un tempo di esecuzione costante rispetto alla crescita del problema (O(1)) sono preferibili rispetto a quelli che crescono linearmente (O(n)) o in modo quadratico (O(n^2)).
Comprensione delle Risorse:
- La dimensione del problema può anche riguardare l’utilizzo delle risorse, come la memoria. Algoritmi efficienti dovrebbero essere in grado di gestire grandi quantità di dati senza esaurire le risorse disponibili.

La Notazione Asintotica

La notazione asintotica è una lingua universale per descrivere il comportamento di un algoritmo mentre la dimensione del problema si avvicina all’infinito. Le tre principali notazioni asintotiche sono:

O Grande (O)
Omega (Ω)
Theta (Θ)

La notazione O Grande descrive il limite superiore di un algoritmo. In sostanza, rappresenta un modo di esprimere il peggior caso di esecuzione di un algoritmo in funzione della dimensione del problema. Ad esempio, se un algoritmo è $O(n^2)$ , significa che il tempo di esecuzione cresce quadraticamente rispetto alla dimensione del problema.

La notazione Omega fornisce il limite inferiore di un algoritmo, indicando il miglior caso possibile in termini di tempo di esecuzione. Se un algoritmo è Ω(n), significa che il tempo di esecuzione cresce almeno linearmente con la dimensione del problema.

La notazione Theta rappresenta il caso medio di esecuzione di un algoritmo. Se un algoritmo è Θ(n), significa che il tempo di esecuzione cresce linearmente con la dimensione del problema.

La notazione O Grande

Per prima cosa diamo una definizione formale della notazione.

Definizione Formale della Notazione O Grande

Sia $g(n)$ una funzione di tempo di esecuzione o spazio, e sia $f(n)$ la funzione associata a un particolare algoritmo.

L’insieme $O(g(n))$ rappresenta l’insieme di tutte le funzioni che crescono al massimo tanto velocemente quanto una costante moltiplicativa di $g(n)$ per valori sufficientemente grandi di $n$ . Formalmente, $f(n)$ è è $O(g(n)$ se esistono costanti positive $c$ e $n_0$ tali che per ogni $n \geq n_0$ , $f(n) \leq c \cdot g(n)$ .

In altre parole, la notazione O Grande fornisce un modo di descrivere il comportamento asintotico di una funzione, ignorando fattori costanti e termini meno significativi quando si considerano input sufficientemente grandi. Essa offre un modo di caratterizzare l’efficienza o la complessità di un algoritmo in modo più generale.

Esempio:

Consideriamo la funzione $f(n) = 3n^2 + 2n + 1$ e la funzione $g(n) = n^2$ . Diremo che $f(n)$ è $O(n^2)$ se esistono costanti positive $c$ e $n_0$ tali che per ogni $n \geq n_0$ , $3n^2 + 2n + 1 \leq c \cdot n^2$ . In questo caso, possiamo scegliere $c = 6$ e $n_0 = 1$ , poiché per ogni $n \geq 1$ , $3n^2 + 2n + 1 \leq 6n^2$ .

Quindi, la definizione formale ci consente di stabilire un legame matematico tra le funzioni e di esprimere la crescita di una funzione in rapporto a un’altra.

Esempi con Grafici in Python

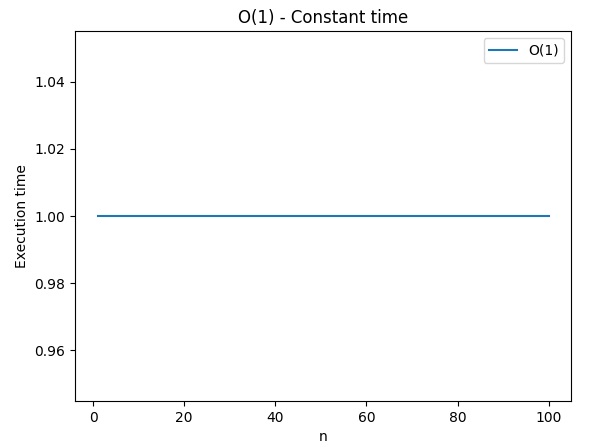
O(1) – Tempo di esecuzione costante

import matplotlib.pyplot as plt
import numpy as np

def example_O_1():
    return 1

n_values = np.arange(1, 101)
time_complexity_values = [example_O_1() for _ in n_values]

plt.plot(n_values, time_complexity_values, label='O(1)')
plt.xlabel('n')
plt.ylabel('Execution time')
plt.title('O(1) - Constant time')
plt.legend()
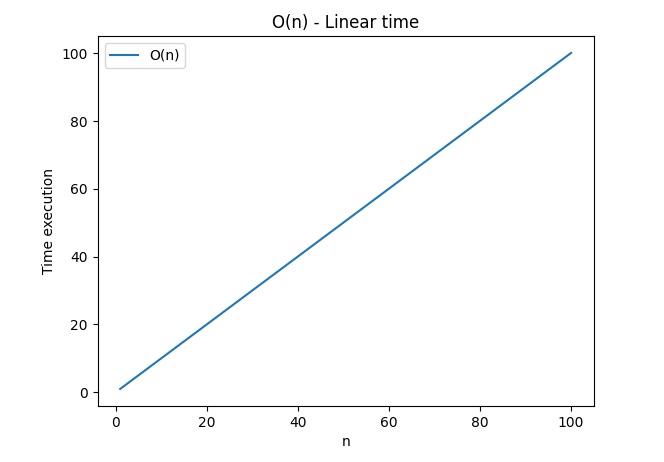
plt.show()

O(n) – Tempo di esecuzione lineare

def example_O_n(n):
    return list(range(n))

plt.plot(n_values, [len(example_O_n(n)) for n in n_values], label='O(n)')
plt.xlabel('n')
plt.ylabel('Execution time')
plt.title('O(n) - Linear time')
plt.legend()
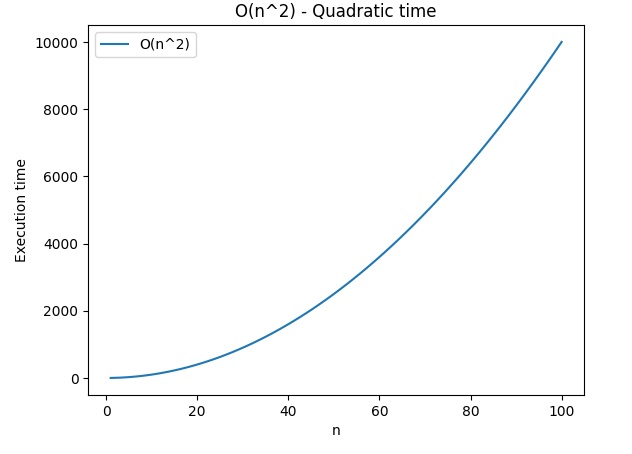
plt.show()

O(n^2) – Tempo di esecuzione quadratico

def example_O_n_squared(n):
    result = []
    for i in range(n):
        for j in range(n):
            result.append((i, j))
    return result

# Plot del grafico
plt.plot(n_values, [len(example_O_n_squared(n)) for n in n_values], label='O(n^2)')
plt.xlabel('n')
plt.ylabel('Execution time')
plt.title('O(n^2) - Quadratic time')
plt.legend()
plt.show()

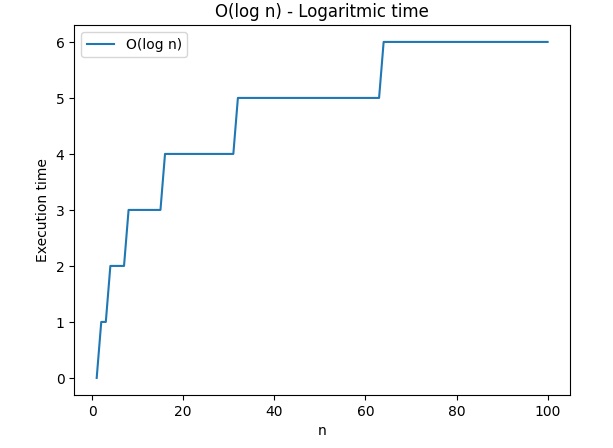
O(log n) – Tempo di esecuzione logaritmico

def example_O_log_n(n):
    return int(np.log2(n))

plt.plot(n_values, [example_O_log_n(n) for n in n_values], label='O(log n)')
plt.xlabel('n')
plt.ylabel('Execution time')
plt.title('O(log n) - Logaritmic time')
plt.legend()
plt.show()

Questi esempi mostrano graficamente come il tempo di esecuzione cambia rispetto alla dimensione del problema, seguendo le diverse complessità indicate dalla notazione O Grande.

Passaggio dalla dimensione del problema alla notazione asintotica

Passare concettualmente dalla dimensione di un problema alla notazione asintotica coinvolge l’analisi dell’andamento dell’algoritmo al crescere della dimensione del problema. La notazione asintotica fornisce un modo di esprimere il comportamento limite di un algoritmo mentre la dimensione del problema si avvicina all’infinito.

Ecco come puoi concettualmente collegare la dimensione di un problema alla notazione asintotica:

Osservazione del Comportamento: Inizia osservando come il tempo di esecuzione o lo spazio richiesto dall’algoritmo cambia in relazione alla dimensione del problema. Chiediti: aumenta linearmente, quadraticamente, logaritmicamente o in un altro modo?
Identificazione del Termine Dominante: Identifica il termine dominante che contribuisce maggiormente alla complessità dell’algoritmo. Questo termine sarà la base della tua notazione asintotica.
Corrispondenza con Notazione Asintotica: Trova la notazione asintotica che meglio descrive il comportamento dell’algoritmo. Ad esempio, se il termine dominante è lineare rispetto alla dimensione del problema, potresti usare la notazione O(n). Se è logaritmico, O(log n), e così via.
Considerazione dei Termini Meno Significativi: Nella notazione asintotica, ciò che conta maggiormente è il termine dominante. I termini meno significativi o le costanti moltiplicative potrebbero essere trascurati. Ad esempio, se hai un algoritmo con complessità 3n^2 + 5n + 7, la notazione asintotica sarà O(n^2).
Verifica delle Proprietà della Notazione Asintotica: Assicurati che la notazione asintotica soddisfi le proprietà fondamentali. Ad esempio, O(n^2) indica che l’algoritmo ha un comportamento quadratico, ma non implica nulla sulle prestazioni specifiche.

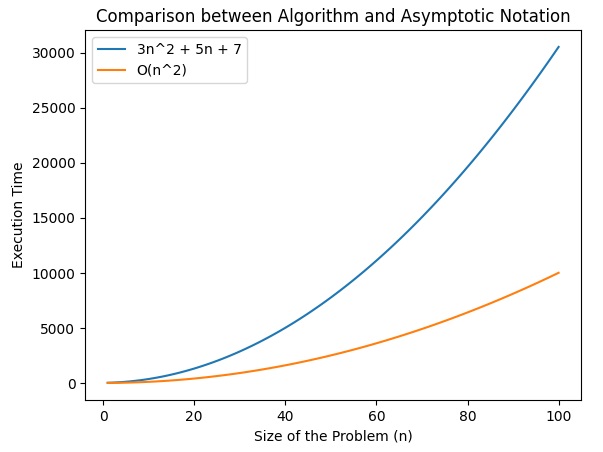
Vediamo un esempio concreto in Python di un algoritmo con complessità (3n^2 + 5n + 7) e il suo confronto con (O(n^2)). Creeremo un grafico per visualizzare il comportamento di entrambi gli andamenti.

import matplotlib.pyplot as plt
import numpy as np

# Algoritmo con complessit&agrave; 3n^2 + 5n + 7
def example_algorithm(n):
    return 3 * n**2 + 5 * n + 7

# Notazione asintotica O(n^2)
def o_notation(n):
    return n**2

# Dimensione del problema
n_values = np.arange(1, 101)

# Calcolo dei tempi di esecuzione
algorithm_values = [example_algorithm(n) for n in n_values]
o_notation_values = [o_notation(n) for n in n_values]

# Plot del grafico
plt.plot(n_values, algorithm_values, label='3n^2 + 5n + 7')
plt.plot(n_values, o_notation_values, label='O(n^2)')
plt.xlabel('Size of the Problem (n)')
plt.ylabel('Execution Time')
plt.title('Comparison between Algorithm and Asymptotic Notation')
plt.legend()
plt.show()

In questo esempio, l’algoritmo è rappresentato dalla funzione (3n^2 + 5n + 7), mentre la notazione asintotica è rappresentata dalla funzione (O(n^2)). Il grafico mostra come il tempo di esecuzione dell’algoritmo cresce quadraticamente rispetto alla dimensione del problema.

Perché viene considerato (O(n^2)):

Nel termine (3n^2 + 5n + 7), il termine dominante che guida la crescita dell’algoritmo è (3n^2) (in quanto ha un esponente maggiore rispetto agli altri).
La notazione asintotica (O(n^2)) cattura il comportamento generale dell’algoritmo, concentrandosi sul termine quadratico mentre la dimensione del problema aumenta.
I termini meno significativi e le costanti moltiplicative vengono trascurati nella notazione asintotica, concentrando l’attenzione sulle caratteristiche fondamentali della crescita dell’algoritmo.

Il grafico mostra come il tempo di esecuzione dell’algoritmo segue un andamento quadratico, supportando la scelta di (O(n^2)) come notazione asintotica appropriata per descrivere la complessità dell’algoritmo.

Conclusione

In questo capitolo, abbiamo gettato le basi per l’analisi degli algoritmi, introducendo concetti chiave come la notazione asintotica e la dimensione di un problema. Questi strumenti ci aiuteranno a valutare le prestazioni degli algoritmi in modo chiaro e a progettare soluzioni ottimali per una vasta gamma di problemi computazionali. Nei capitoli successivi, esploreremo applicazioni pratiche di questi concetti, affrontando esempi concreti e approfondendo la nostra comprensione dell’arte e della scienza dietro la progettazione degli algoritmi.