Mathematica al succo di lampone - Meccanismo Complesso

Post Views: 17.737

Avevate mai considerato che Rasperry Pi e Mathematica potessero lavorare insieme?

Recentemente ho scritto un articolo su electroYou riguardo questo argomento, e mi è stato proposto di riproporlo alla community Meccanismo Complesso. Spero che questo articolo possa suscitare l’interesse per tutti coloro che si interessano al mondo della modellistica o anche per chi si affaccia per la prima volta al mondo di Raspberry Pi.

In questo articolo spiegherò che hardware serve, come scaricare questo software, come installarlo e come utilizzarlo.

Chiunque sia intenzionato a farlo può scaricare ed installare l’ultima release di Mathematica dal sito della Wolfram Foundation gratuitamente, sul proprio Raspberry Pi.

Si tratta di una versione non limitata, con tutte le 5000 e oltre funzioni di Mathematica funzionanti, senza scadenza e con funzioni speciali pensate appositamente per il Raspberry Pi. E’ possibile far funzionare Mathematica dal proprio Raspberry Pi in modalità testuale, da terminale locale o remoto, in modalità grafica, locale o remota e in modalità kernel-remoto, pur essendo, quest’ultima, subordinata all’acquisto di una versione in licenza per PC di Mathematica.

Cosa acquistare per usare Mathematica sul Raspberry Pi

Componentistica principale

Un Raspberry Modello B (con connettore di rete Ethernet e 512MB di memoria a bordo), circa 35€.
Un alimentatore da parete micro USB che eroghi 5V stabilizzati e almeno 1A, pochi €.
Una scheda SD da almeno 16GB di memoria (meglio se 32GB, lavorando con Mathematica vi accorgerete che la scheda SD è come la pista di decollo/atterraggio per i piloti di aereo: non è mai troppa). Più la scheda SD che acquisterete sarà veloce, più il Raspberry Pi sarà veloce: acquistatene una con un Transfer Rate di almeno 30MB/s in lettura, vi assicuro che non ve ne pentirete, da 10 a 20 €;
Un case (anche di plastica, giusto per protezione) per il vostro nuovo Raspberrino!
Qualora intendiate utilizzare il GPIO, assicuratevi di acquistarne uno che abbia la feritoia di uscita laterale per il flat cable, altrimenti dovrete poi ricavarla tagliando un lato del contenitore, da 5€ se di plastica a 50 € per l’alluminio.

raspberry_mathematica — Fig.1: Contenitore PiBow con feritoia, ma ce ne sono di molti altri tipi

Cavi e Connettori

Se userete il Raspberry Pi come terminale potete collegarlo al router di casa con un semplice cavo RJ45. Potete anche collegarlo direttamente al vostro PC, utilizzando indifferentemente cavi di tipo Straight o Crossed, in quanto i PC moderni capiscono quale tipo di cavo è stato utilizzato e si adattano di conseguenza. Solo nel caso in cui abbiate un PC molto vecchio dovrete utilizzare un cavo di tipo Crossed. In questo caso non vi serve altro. Questa è la configurazione che ho adottato anche io, perchè lo utilizzo in remoto tramite SSH (console) o tramite RDP (Remote Desktop).

Se invece volete utilizzare il Raspberry Pi da solo (come computer stand alone, in pratica) oltre al cavo RJ45 vi serviranno anche una tastiera e un mouse USB (in questo caso potrebbe essere utile comperare un HUB USB, poichè il Raspberry Pi ha solo due slot USB e avere uno slot USB libero per salvare i dati su una chiavetta potrebbe rivelarsi molto utile), infine vi servirà anche un cavo HDMI oppure un cavo per segnale videocomposito per collegare l’uscita video al TV di casa.

Durante la procedura di installazione, tuttavia, dovrete per forza utilizzarlo da solo, non essendo ancora disponibili i servizi remoti.

Se volete utilizzare il Raspberry Pi per fare qualche esperimento su breadboard sarebbe meglio acquistare anche un adafruit!, per un costo di due o tre euro, in pratica un piccolo PCB (vedi Fig. 2):

raspberry_mathematica02 — Fig.2: un adafruit!

Se invece volete lavorare su millefori, è sufficiente acquistare un connettore IDC a 26 poli.

In entrambi i casi vi servirà anche un pezzo di flat cable (vedi Fig.3) intestato alle estremità con due connettori IDC da flat a 26 poli, potete costruirvelo o acquistarlo già intestato al prezzo di uno o due euro.

raspberry_mathematica03 — Fig.3: flat cable a 26 poli con 2 connettori IDC

Direi che la spesa è fatta e, in fin dei conti, non si è speso molto!

Introduzione a Mathematica

Spiegare che cosa sia Mathematica in poche righe è davvero impossibile.

Come mai aziende leader di mercato sono disposte a pagare quasi 10k$ ogni 16 kernel di questo pacchetto (la soluzione di un moderno problema di calcolo tensoriale su equazioni differenziali non lineari alle derivate parziali richiede molti kernel di calcolo fortemente parallelo, per essere eseguito in tempi accettabili, utilizzando macchine molto potenti), senza contare tutti gli add-on e i pacchetti di calcolo opzionali e di assistenza agli sviluppatori che vengono venduti a parte?

Semplicemente perchè… non comprandolo spenderebbero di più!

Oggi la modellistica matematica permette di fare previsioni molto accurate e potenti, relativamente al problema fisico in oggetto di studio, ma necessita di prodotti software altrettanto accurati e potenti, che siano in grado di effettuare calcoli in modalità anche simbolica, che integrino un linguaggio di programmazione evoluto, che si possano interfacciare a linguaggi quali il C o il C++, che possano lavorare in parallelo scomponendo il problema in pezzi semplici ed interagire in modo intelligente affinchè risultati parziali trovati da una macchina non debbano essere ricalcolati da un’altra macchina, il tutto mentre il calcolo è ancora in corso.

Mathematica è tutto questo: è un ambiente di calcolo numerico e simbolico, è un potente linguaggio interpretato, sia logico che funzionale ed effettua il riconoscimento di schemi: il pattern-matching. Praticamente tutte le librerie di funzioni interne, poi, possono essere utilizzate per creare nuovi pacchetti per espandere le funzioni interne di Mathematica stesso.

Immaginate che cosa è diventato Mathematica, quindi, nel corso degli anni, dalla sua prima versione del 1988 ad oggi, con centinaia di programmatori in tutto il mondo che hanno costantemente continuato a svilupparne le funzioni…

E oggi… possiamo legalmente utilizzarlo in modo gratuito o, al massimo, al prezzo di un Lampone!

Installazione di Mathematica sul Raspberry Pi

Per potere installare Mathematica sul vostro Raspberry Pi dovete installare il sistema operativo Raspbian.

Coloro che hanno acquistato una scheda SD preformattata insieme al Raspberry Pi troveranno Mathematica all’interno del pacchetto di installazione software NOOB. Il pacchetto è anche scaricabile direttamente dal sito della Raspberry Foundation. In questo caso è sufficiente seguire le istruzioni di installazione dopo aver avviato il Raspberry con la SD inserita (ricordatevi però di fare un backup prima!).
Se invece avete già il sistema operativo installato, ma non mathematica, non è assolutamente il caso di reinstallare tutto da capo, basta seguire queste semplici istruzioni: 1. Come prima cosa aggiorniamo i vari pacchetti del nostro Raspberry alla release più recente (sarebbe opportuno fare questa operazione, ogni tanto) digitando: sudo apt-get update && sudo apt-get upgrade Mettete in conto che se è la prima volta, dopo l’installazione, che effettuate questo aggiornamento, ci potrebbe volere anche molto tempo prima che il Raspberry Pi completi l’operazione.
E’ possibile che il Raspberry Pi vi chieda una conferma di installazione, durante la procedura, a cui risponderete Y. 2. Una volta terminato l’aggiornamento possiamo passare ad installare Mathematica, con il comando: sudo apt-get install wolfram-engine A questo punto non vi resta che confermare e… attendere pazientemente!

Terminata l’installazione, ricordatevi di fare il secondo backup della scheda.
A proposito, dato che per fare i backup dovrete spegnere il sistema ed estrarre la scheda SD, vi ricordo che il modo corretto di arrestare il Raspberry Pi è quello di digitare il comando:sudo poweroff

Specialmente se siete in erba, avere un backup in più vi permetterà di risparmiare molto tempo se inavvertitamente combinate qualche guaio!

Mathematica

Primo sguardo

Ora abbiamo una versione completa e funzionante di Mathematica, evviva!
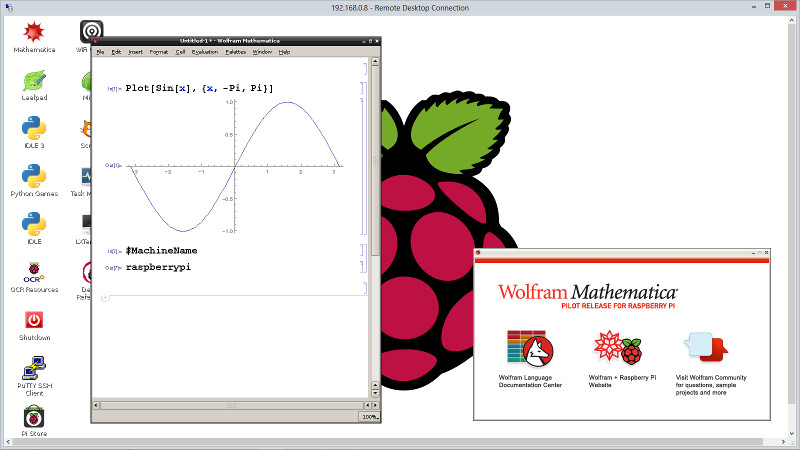
Il desktop del Raspberry Pi è grossomodo questo:

raspberry_mathematica05 — Fig.4: desktop di Raspberry

La prima icona in alto a sinistra è Mathematica. Avviamolo!!

Dopo aver avviato Mathematica (ci vorrà qualche secondo perchè Mathematica carichi tutti i moduli) compariranno due finestre (vedi Fig.5).
La prima finestra è chiamata Notebook (sulla sinistra) e permette di immettere i comandi e visualizzare le risposte fornite dal kernel, che è una applicazione testuale che viene avviata di nascosto e contiene il motore del programma. Sulla destra avete un’altra finestra che viene chiamata Helper ed è sostanzialmente una finestra di aiuto. E’ comunque molto comoda da avere.

raspberry_mathematica06 — Fig.5: le finestre Notebook e Helper sul desktop

Il primo comando

Se provate a digitare il comando:$MachineName

otterrete come risposta raspberrypi.
In pratica avete chiesto a Mathematica di dirvi su che macchina sta girando il kernel e lui vi ha risposto che sta girando sul Raspberry Pi. Non è detto che debba sempre essere così.

Il primo grafico

Come seconda prova potete digitare il comando:Plot[Sin[x],{x,-Pi,Pi}]

Otterrete un grafico della funzione sin(x) tra -π e π (vedi la finestra Notebook in Fig.5).
Con la funzioneTiming[]

potrete misurare il tempo impiegato da Mathematica per effettuare il calcolo richiesto.
Questa funzione diventa quindi estremamente comoda per fare qualche confronto sul tempo di calcolo impiegato su un PC e su un Raspberry Pi. Digitando:Timing[Plot[Sin[x],{x,-Pi,Pi}]]

si scopre che il tempo di calcolo sul mio PC (Intel i7-3520M 2.9GHz,12GB RAM,Windows 8 64bit) è di 0.015s, mentre sul Raspberry Pi (B type) è di 0.53s.
Ovviamente il Raspberry Pi è molto più lento, ma è comunque usabile.
Facciamo qualcosa di più complicato, per esempio un disegno in 3D, e misuriamo il tempo necessario all’operazione. Digitiamo:Timing[Plot3D[Sin[x^2 + y^2], {x, -Pi, Pi}, {y, -Pi, Pi}]]

Otteniamo:

raspberry_mathematica07 — Fig.6: il portauovo

Il collage rivela che il mio PC impiega 0.078s, mentre il Raspberry Pi 3.21s. Non male, tutto sommato.

Un diagramma di Bode

Proviamo a fare qualcosa di ancora più impegnativo, per esempio un diagramma di Bode. Scelgo di plottare le due funzioni, in modulo e fase:

Inseriamo il codice:

Timing[
    BodePlot[
      {1/(s (s + 10)), ((s + 1))/((s + 100) (s + 10000)) }, 
      plotLabel -> {"Magnitude Plot", "Phase Plot"}, 
      ImageSize -> 550,
      Frame -> True, 
      PlotStyle -> {Directive[Thick, ColorData[20, 1]], Directive[Thick, ColorData[20, 9]]}, 
      Frame -> False, 
      AspectRatio -> 1/2.25, 
      GridLines -> Automatic, 
      GridLinesStyle -> Directive[GrayLevel[0.7],Dashed]
    ]
]

Timing:

Raspberry = 5.14s
PC = 0.094s

Un diagramma di Nyquist

Proviamo a fare il diagramma di Nyquist per la prima funzione di trasferimeto:

Timing[
     NyquistPlot[1/(s (s + 10)), 
         ImageSize -> 250, 
         Frame -> True, 
         PlotStyle -> {Directive[Thick, ColorData[20, 1]], 
         Directive[Thick, ColorData[20, 9]]}, 
         Frame -> False, 
         GridLines -> Automatic, 
         GridLinesStyle -> Directive[GrayLevel[0.7],Dashed]
        ]
]

Timing:

Raspberry = 5.99s
PC = 0.11s

Un diagramma di Nichols

Plottiamo anche il diagramma di Nichols:

Timing[
  NicholsPlot[1/(s (s + 10)), 
    ImageSize -> 350, 
    Frame -> True, 
    PlotStyle -> {Directive[Thick, ColorData[20, 1]], 
    Directive[Thick, ColorData[20, 9]]}, 
    Frame -> False, 
    GridLines -> Automatic, 
    GridLinesStyle -> Directive[GrayLevel[0.7], Dashed]
    ]
]

Timing:

Raspberry = 1.84s
PC = 0.031s

Risolvere equazioni differenziali lineari alle derivate ordinarie

Proviamo ora a risolvere una equazione differenziale lineare di primo ordine, per esempio troviamo la tensione ai capi di un condensatore a cui viene applicato un gradino di tensione tramite un generatore di tensione reale.

Il codice da inserire in Mathematica è:

Clear[Tau];
Clear[E1];
Timing[
 f = Vc[t] /. 
   Simplify[
     DSolve[{Vc'[t] == (E1 - Vc[t])/Tau, Vc[0] == 0}, Vc[t], t]][[1]];
 E1 = 12;
 Tau = 0.1;
 Plot[f, {t, 0, 1},
  ImageSize -> 550,
  AxesLabel -> {"t", "Vc(t)"},
  PlotStyle -> Directive[Thick, ColorData[20, 1]],
  Frame -> False,
  AspectRatio -> 1/GoldenRatio,
   GridLines -> Automatic,
   PlotRange -> {0, 13},
   GridLinesStyle -> Directive[GrayLevel[0.7], Dashed],
   AxesStyle -> {Directive[Blue, 15], Directive[Blue, 15]}
   ]
  ]
Clear[Tau];
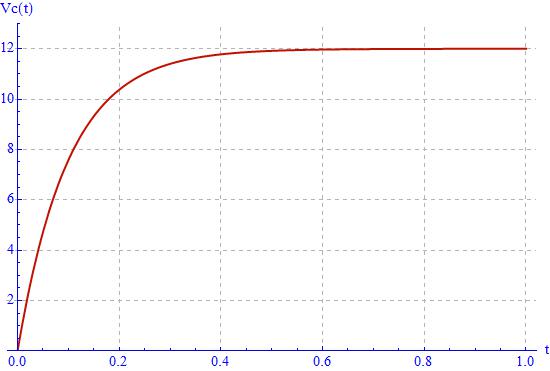
Clear[E1];

Nell’ipotesi di un generatore con una tensione di 12V e una costante di tempo pari a 100ms si ottiene questo grafico:

Analizzando il codice si può osservare che ho fatto ricavare a Mathematica la soluzione simbolicamente, infatti, stampandola si ottiene:

V_C(t)=E_1\left(1- e^{-\frac{t}{\tau}} \right )

Analizziamo ora i tempi di calcolo:

Raspberry = 2.51s
PC = 0.015s

Se invece la forzante è cosinusoidale per t>0 e nulla in precedenza si ha che:

Clear[Tau];
Clear[Omega];
Clear[Vmax];
Timing[
 f = Vc[t] /. 
   Simplify[
     DSolve[{Vc'[t] == (Vmax*Cos[Omega*t] - Vc[t])/Tau, Vc[0] == 0}, 
      Vc[t], t]][[1]];
 Vmax = 230;
 Tau = 0.001;
 Omega = 314;
 Plot[{f, Vmax*Cos[Omega*t]}, {t, 0, 0.04},
  ImageSize -> 550,
  AxesLabel -> {"t", "Vc(t)"},
  PlotStyle -> {Directive[Thick, ColorData[20, 1]], 
    Directive[Dotted, ColorData[1, 2]]},
  Frame -> False,
  AspectRatio -> 1/GoldenRatio,
   GridLines -> Automatic,
   GridLinesStyle -> Directive[GrayLevel[0.7], Dashed],
   AxesStyle -> {Directive[Blue, 15], Directive[Blue, 15]}
   ]
  ]
Clear[Tau];
Clear[Omega];
Clear[Vmax];

ponendo:

Vmax = 230 V;
Tau = 0.001 s;
Omega = 314 rad/s;

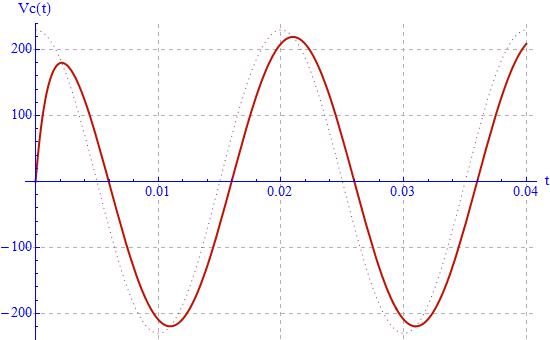
si ottiene:

Si può osservare che la linea tratteggiata corrisponde alla tensione impressa al circuito dal generatore. Analizziamo ora i tempi di calcolo:

Raspberry = 3.78s
PC = 0.093s

La soluzione trovata da Mathematica è:

V_C(t)=\text{Vmax}\frac{\omega \tau \sin (\omega t)+\cos (\omega t)-e^{-\frac{t}{\tau}}}{\omega^2 \tau^2+1}

Parametrizzazioni, animazioni e LPDE

Supponiamo, per esempio, di avere risolto l’equazione delle onde e voler capire un po’ come stanno le cose dal punto di vista fisico.
Il comando Manipulate permette di giocare con i parametri di una equazione fornendo dei cursori. Ogni tanto lo uso, specialmente quando devo capire cosa diavolo significhi l’equazione che ho appena risolto…
Proviamo ad immettere questo codice:

Manipulate[
 Show[
  Plot[
   Cos[1*t - x/\[Lambda]], {x, -5, 0},
   PlotRange -> {{-5, 5}, {-2, 2}},
   PlotStyle -> Black],
  Plot[\[CapitalGamma]*Cos[1*t + x/\[Lambda]], {x, -5, 0},
   PlotRange -> {{-5, 5}, {-2, 2}},
   PlotStyle -> Red],
  Plot[(1 - \[CapitalGamma]) Cos[1*t - x/\[Lambda]], {x, 0, 5},
   PlotRange -> {{-5, 5}, {-2, 2}},
   PlotStyle -> Blue],
  ImageSize -> {400, 300}],

 {{\[Lambda], 1, "wavelength \[Lambda]"}, .1, 5, ImageSize -> Tiny},
 {{\[CapitalGamma], .1, "reflection coefficient \[CapitalGamma]"}, 0, 
  1, ImageSize -> Tiny},
 {{t, 0, "time"}, 0, Infinity, ControlType -> Trigger},
 AutorunSequencing -> {2, 3, 4}]

Otterremo una finestra di questo tipo:

raspberry_mathematica15 — Fig.7: il comando Manipulate genera dei cursori

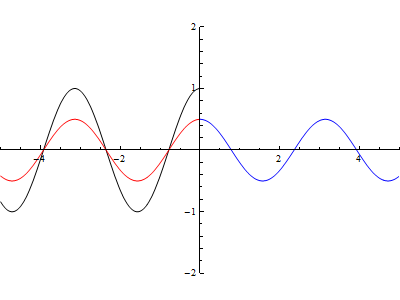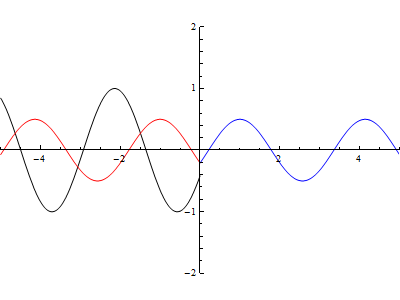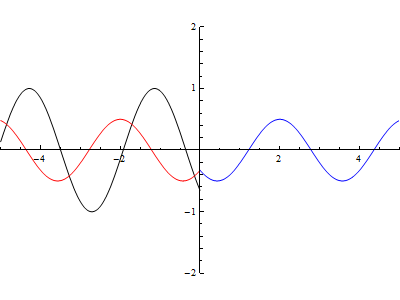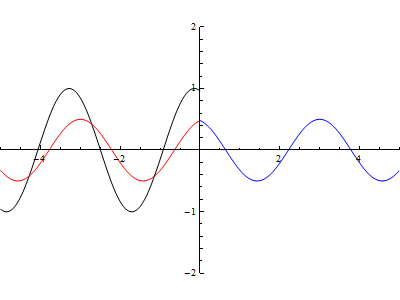
Da come potete vedere in Fig.7, in x=0 si ha una discontinuità, l’onda disegnata in nero è l’onda incidente, quella in rosso è l’onda riflessa, mentre in blu si ha l’onda trasmessa.
Variando i cursori che avete a disposizione potete osservare cosa succede cambiando la lunghezza d’onda e il coefficiente di riflessione. Premendo il pulsante (play)otterrete una animazione in funzione dei parametri impostati.
Per avere una idea di quello che potete ottenere ecco una animazione effettuata ponendo il coefficiente di riflessione pari a 0.5:

raspberry_mathematica_16 — Fig.8: Soluzione grafica dell’equazione monodimensionale delle onde con coefficiente di riflessione pari a 0.5

Timing:

Raspberry Pi = 0.02s
PC < eps (in pratica mi da zero)

Matrici

Un problema che avevo risolto era stato l’inversione di una matrice del tipo:

Per sfortuna Mathematica non può ancora invertire questa matrice al variare della sua dimensione trovando una formula generale per farlo, però può essere di grande aiuto per verificare la bontà della soluzione trovata.

Impostando la funzione contenente la soluzione:

f[n_, i_, j_] := 1/3*(1/2^(Abs[i - j]) - 1/(2^(2*n + 2 - i - j)))
M[k_] := Table[f[k, i, j], {i, 1, k}, {j, 1, k}]

Possiamo divertirci a costruire una matrice inversa di ordine n scrivendo M[n]. Esempio:

Vediamo se invertendo la matrice inversa si riottiene la matrice principale. Tra l’altro facendo così possiamo fare un piccolo grafico circa i tempi di calcolo.

Direi che funziona. A questo punto possiamo utilizzare la matrice per effettuare un piccolo programmino per misurare i tempi di esecuzione e fare un grafico. Come prima cosa vediamo come creare i vari punti. Ho dato il comando:

vaio = Table[{n, Timing[Inverse[M[n]];][[1]]}, {n, 1, 50}]

sul mio PC e il comando:

raspi = Table[{n, Timing[Inverse[M[n]];][[1]]}, {n, 1, 50}]

sul Raspberry Pi, che è lo stesso comando dato sul mio PC, con la differenza che il vettore risultante è stato chiamato raspi…
Chi fino qui ha studiato tutti i vari comandi che ho utilizzato noterà che vaio o raspi sono due matrici contenenti nella prima colonna la dimensione della matrice da invertire e, nella seconda colonna, il tempo impiegato ad invertirla. In pratica ho la matrice di punti (x,y), utili per fare il grafico che cercavo.
Per farlo useremo il comando ListLinePlot:

ListLinePlot[
 {vaio, raspi},
 ImageSize -> 550,
 AxesLabel -> {"n", "t (s)"},
 PlotStyle -> {Directive[Thick, ColorData[55, 1]], 
   Directive[Thick, ColorData[20, 1]]},
 Frame -> False,
 AspectRatio -> 1/GoldenRatio,
  GridLines -> Automatic,
  GridLinesStyle -> Directive[GrayLevel[0.7], Dashed],
  AxesStyle -> {Directive[Blue, 15], Directive[Blue, 15]},
 PlotLegends -> {"PC", "Raspberry Pi"}
 ]

Il cui risultato è:

mathematica-raspberry-curve — Fig.9: Vaio vs Raspi

Chiaramente il PC vince a mani basse, (infatti serve una licenza a pagamento di Mathematica, Stephen Wolfram fa dei bei regali ma non è scemo) ma guardando meglio il grafico è possibile notare che in 2.2s circa posso invertire una matrice 40×40 e, se sono disposto ad aspettare 6 secondi, posso invertirne una 50×50. Tutto sommato non è così male.

Chiaramente se dovessi invertire una matrice 200×200 avrei certamente bisogno di utilizzare un PC (che ci impiegherebbe 14.62s. il Raspberry, stimando dal grafico, impiegherebbe più di 13 minuti per calcolarla).
Da notare che il grafico sale, in entrambi i casi, come il cubo di n, che è l’ordine di grandezza di tempo richiesto all’algoritmo per invertire le matrici.

Comandi Mathematica per Raspberry PI

Modalità superuser

Stephen Wolfram ha voluto omaggiare gli affezionati al Lampone con delle funzioni specifiche, che permettono di accedere all’hardware di sistema del Raspberry Pi. E’ necessario, però, per poter accedere a queste funzioni, lanciare Mathematica in modalità amministratore, in quanto dovrà avere accesso alle risorse hardware. Dobbiamo quindi creare un’icona sul desktop del Raspberry per lanciare Mathematica in modalità amministratore:

Clicchiamo con il tasto sinistro sopra l’icona di mathematica (una volta sola);
Premiamo CTRL+C e poi CTRL+V;

comparirà una finestra come questa:

raspberry_mathematica17 — Fig.10: Giusto davanti al lampone deve finire?

Cambiamo la stringa da Wolfram-Mathematica.desktop in Wolfram-Mathematica-sudo.desktop e clicchiamo su Rename, che nel frattempo è diventato selezionabile;

Clicchiamo quindi con il tasto destro sulla nuova icona creatasi e, dal menu che comparirà clicchiamo su Leafpad (dovrebbe essere la seconda voce in alto);
Si aprirà un editor di testo con il seguente contenuto:

[Desktop Entry]
Version=1.0
Type=Application
Name=Mathematica
Comment=Technical Computing System
TryExec=mathematica
Exec=/opt/Wolfram/WolframEngine/10.0/Executables/mathematica %F
Icon=wolfram-mathematica
MimeType=application/mathematica;application/vnd.wolfram.cdf;application/mathematicaplayer
Categories=Application;Education;

Modificate la quarta riga con: Name=MathemSudo

e la settima con: Exec=sudo /opt/Wolfram/WolframEngine/10.0/Executables/mathematica %F

Salvate ed uscite.
Adesso avete a disposizione una icona per lanciare Mathematica in modalità amministratore.

Un semplice circuito

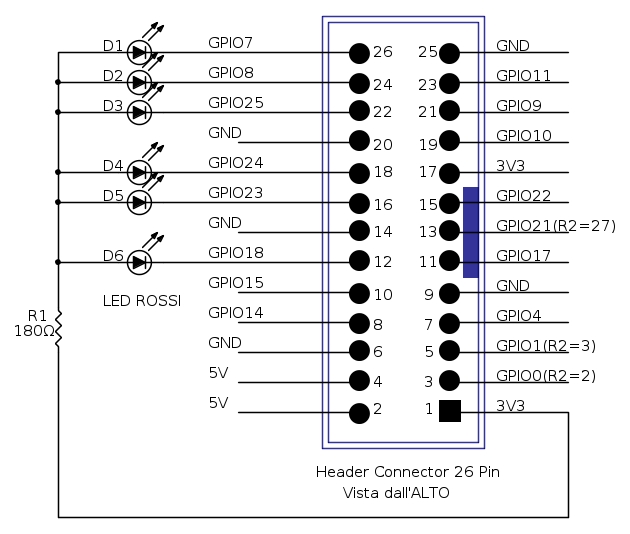
Come prima cosa proviamo a pilotare dei led che andremo a collegare sulla porta GPIO del Raspberry.
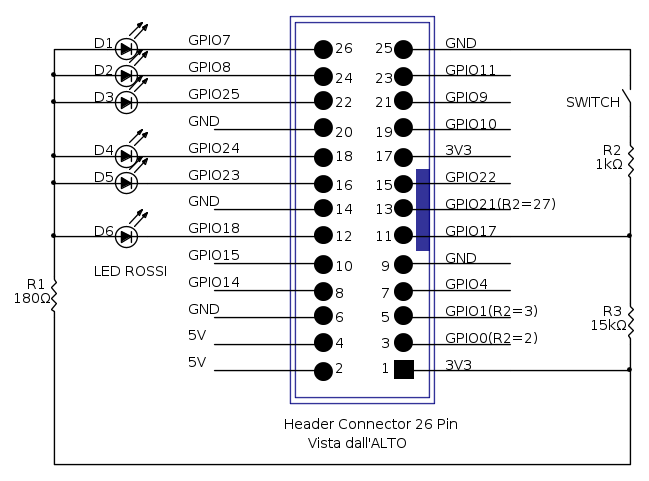
Si tratta di individuare questo connettore di espansione:

Dopodichè collegheremo al GPIO il pezzo di flat cable che ci siamo procurati in precedenza. L’altro capo del connettore andrà collegato alla schedina adafruit!,anch’essa acquistata in precedenza. Dovremmo ottenere un risultato di questo tipo:

raspberry_mathematica19 — Fig.12: Non si vede tutto il casino che ho sulla scrivania, vero?

Il risultato sembra essere un lavoro pulito ed ordinato, senza fili volanti che potrebbero staccarsi e magari dare origine a qualche cortocircuito.

A tal proposito, è bene fare molta attenzione a lavorare con i pin del GPIO, in quanto il processore A11 presente sul Raspberry Pi non è fatto per gestire I/O in modo “pesante”, come viene, per esempio, implementato su un PIC o un AVR. Un A11 è, di fatto, un microprocessore a tutti gli effetti, non un microcontrollore.
Per cui, fate molta attenzione, se collegate un pin a massa e lo configurate per funzionare come uscita e ci scrivete un uno logico semplicemente lo rovinate in modo irreparabile, stessa cosa se ci scrivete uno zero logico e lo collegate a V_dd.
Inoltre il microprocessore lavora a 3.3V e nessuno degli I/O è 5V tolerant, per cui, come prima, se configurate un I/O per funzionare da ingresso e poi lo collegate a 5V, semplicemente rovinerete il vostro Raspberry Pi. Gli output possono fornire ognuno non più di 16mA, e tutti insieme non più di 40mA, per cui accenderemo un solo led (rosso) per volta con una resistenza comune a tutti i led pari a 180Ω.
Passiamo quindi al circuito vero e proprio. Dovete realizzare questo schema:

mathematica-raspberry-header — Fig.13: Header Conenctor realizzato con FidoCadJ

In Fig.14 invece vi mostro come ho effettuato il montaggio. Ho cercato di essere più ordinato possibile:

Fig.12: circuito montato con 6 LED — Fig.14: circuito montato con 6 LED

La funzione chiave che è stata resa disponibile su Mathematica, per scrivere su un pin del Raspberry PI è:DeviceWrite["GPIO", numero_del_pin -> 1_o_0]

Come prima cosa organizziamo i pin, sui quali vogliamo scrivere, in un vettore ordinato:pins = {7, 8, 25, 24, 23, 18};

Poi sarà sufficiente prendere l’elemento i-esimo del vettore per far accendere il led corrispondente. Molto semplicemente possiamo ricorrere al buon vecchio comando Manipulate, già incontrato in precedenza.
Il codice diventa:

pins = {7, 8, 25, 24, 23, 18};
Do[DeviceWrite["GPIO", pins[[i]] -> 1], {i, Length[pins]}];
previous = 1;
LEDs[i_] := {
   DeviceWrite["GPIO", pins[[previous]] -> 1];
   DeviceWrite["GPIO", pins[[i]] -> 0];
   previous = i;
   };
Manipulate[LEDs[i], {i, 1, Length[pins], 1}]

La seconda riga, cioè il comando Do[], serve per far spegnere tutti i led (mettendo l’uscita a 1 il led si spegne, per come è collegato). La terza riga imposta la variabile previous a 1 e serve per fare in modo che, una volta avviato il ciclo, il led acceso in precedenza possa essere spento. La quarta riga contiene la funzione LEDs, che si occupa di spegnere il led precedente, accendere quello richiesto e memorizzare il led acceso nella variabile previous, in modo da poterlo spegnere alla successiva chiamata. L’istruzione Manipulate, infine, ci permette di impostare il ciclo come vogliamo.

Eseguendo il codice verrà visualizzata questa finestra:

mathematica-raspberry-finestra1 — Fig.15: Finestra manipulate

Se spostiamo il cursore vedremo accendersi il LED corrispondente. Se clicchiamo sul + indicato dalla freccia:

mathematica-raspberry-finestra2 — Fig.16: Cliccami!

Vedremo comparire un piccolo menu molto utile:

mathematica-raspberry-finestra3 — Fig.17: menu funzioni extra

Spieghiamolo da sinistra a destra:

Nell’area di testo è possibile scrivere un numero, da 1 a 6, corrispondente al numero del led da far accendere;
Cliccando sul – si decrementa di una unità il numero scritto nell’area di testo;
Il simbolo , Play, anima i led facendo muovere la barra in automatico;
Cliccando sul + si incrementa di una unità il numero scritto nell’area di testo;
Cliccando sulle doppie frecce verso l’alto si aumenta la velocità di scansione dei led;
Cliccando sulle doppie frecce verso il basso si diminuisce la velocità di scansione dei led;
L’ultimo simbolo permette di commutare tra scansione in avanti, scansione all’indietro e scansione biderezionale.

Leggere lo stato di un pin

Per leggere lo stato di un pin possiamo utilizzare la funzione:DeviceRead["GPIO", pin_da_leggere]

Montiamo il seguente circuito (oppure aggiungiamo la parte mancante al precedente):

mathematica-raspberry-fidocadj — Fig.18: Header connector 26 Pin

Ho inserito una resistenza anche in serie al pulsante/interruttore per evitare, nel caso in cui sbagliassimo a impostare il GPIO del Raspberry Pi e lo configurassimo come uscita, invece che come ingresso, di rovinare il port.

Nel caso in cui volessimo utilizzare un pin come uscita, è possibile scrivere direttamente sul port il valore da impostare. Non è così, invece, nel caso in cui volessimo leggere lo stato di un bit.
Questo perchè, di default, i pin GPIO vengono impostati come uscite.
E’ necessario, in questo caso, configurare il bit come ingresso, con l’istruzione:DeviceConfigure["GPIO", bit_da_impostare -> "Input"]

Se avessimo un vettore sarebbe necessario scandirlo con una istruzione Do.
Per esempio questo programmino configura i bit dei LED come ingressi, li legge e riempie un vettore con la scansione della lettura:

sw = 1; i = 1;
pins = {7, 8, 25, 24, 23, 18};
inputs = ConstantArray[-1, Length[pins]];
Do[
 DeviceConfigure["GPIO", pins[[i]] -> "Input"];
 inputs[[i]] = pins[[i]] /. DeviceRead["GPIO", pins[[i]]];
 , {i, Length[pins]}]
inputs

Questo programma invece configura nuovamente tutti i bit dei LED come uscite, e li pone ad 1:

pins = {7, 8, 25, 24, 23, 18};
Do[
 DeviceConfigure["GPIO", pins[[i]] -> "Output"];
 DeviceWrite["GPIO", pins[[i]] -> 1];
 , {i, Length[pins]}]

Facciamo adesso un programmino che faccia accendere i led in sequenza fino a quando non si prema il tasto:

sw = 1; i = 1;
pins = {7, 8, 25, 24, 23, 18};
DeviceConfigure["GPIO", 17 -> "Input"]
While[sw == 1,
 sw = 17 /. DeviceRead["GPIO", 17];
 DeviceWrite["GPIO", pins[[i]] -> 1];
 If[i < Length[pins], i++, i = 1];  DeviceWrite["GPIO", pins[[i]] -> 0];
 Pause[0.2];
 ]
DeviceWrite["GPIO", pins[[i]] -> 1];

Non è il modo migliore per farlo, ma certamente è il più semplice.

Importare immagini dalla telecamera per Raspberry Pi

Il Raspberry Pi ha un connettore appositamente predisposto per ospitare una piccola telecamera.
Ne esistono due modelli, una da 5Mpixel 1080p:

mathematica-raspberry-connettore1 — Fig.19: Telecamera 5Mpixel 1080p

e una per la visione notturna, sempre da 5Mpixel 1080p:

mathematica-raspberry-connettore2 — Fig.20: Telecamera IR 5Mpixel 1080p

Ecco una immagine del Raspberry con la telecamera nel suo connettore:

mathematica-raspberry-connettore3 — Fig.21: Raspi and Camera just married

Mathematica permette di acquisire una immagine dalla fotocamera con il comando:image1 = DeviceRead["RaspiCam"];

A questo punto nella variabile image1 avete l’immagine e potete manipolarla utilizzando un comando qualunque di Mathematica.

Comunicazioni in seriale RS232

Mathematica per Raspberry Pi può dialogare con la porta seriale presente sul connettore GPIO (pin 8,TX e pin 10,RX).
ATTENZIONE: non collegate direttamente una seriale qualsiasi a questi pin, che lavorano a 3.3V, senza traslare i livelli o rovinerete il Raspberry Pi.
Come prima cosa è necessario aprire la porta di comunicazione. Possiamo utilizzare il comando:serial = DeviceOpen["Serial",{"/dev/ttyUSB0","BaudRate"->9600}]

Potete sostituire 9600 con il BaudRate necessario (da 476 Baud fino a 31.25MBaud). 115200 è il BaudRate di default.
A questo punto è possibile leggere una stringa di dati dalla seriale:data = DeviceReadBuffer[serial,"String"]

Il comando leggerà dalla seriale aperta in serial e ne riempirà la stringa data con il buffer.
oppure è possibile scrivere una stringa sulla seriale:DeviceWriteBuffer[serial,data]

Il comando scriverà sulla seriale aperta in serial la stringa data.

Mathematica in modalità kernel remoto

Se avete seguito gli esempi che ho illustrato fino qui, provandoli direttamente su Mathematica fatto girare sul vostro Raspberry Pi, avrete notato che se vi collegate al Raspberry in RDP (con, per esempio, Windows Remote Desktop) la velocità di dialogo con il desktop non è entusiasmante, mentre le cose migliorano molto se avete il Raspberry Pi collegato alla TV di casa e lo utilizzate con la sua tastiera e il suo mouse.
Mathematica permette, qualora abbiate anche una versione su PC, di utilizzare il front-end (la sola interfaccia grafica) presente sul vostro PC, ma il Kernel del Raspberry, collegandosi in remoto.
Vediamo come fare per avere accesso a questo strumento.
Dopo aver aperto Mathematica sul vostro PC, andate su Evaluation e poi su Kernel Configuration Options.
Si aprirà questa piccola finestra:

mathematica-raspberry-finestra4 — Fig.22 piccole finestre per grandi kernel

Cliccate su Add.

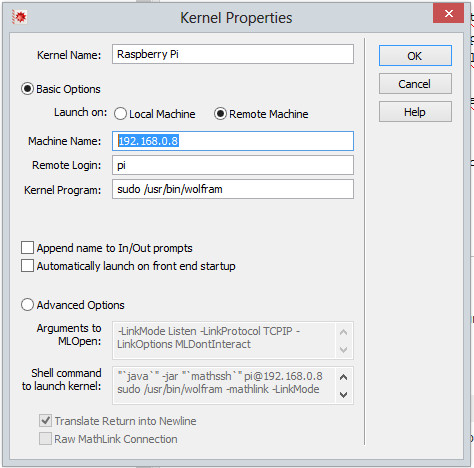
A questo punto dovrete compilare il form che appare copiando dall’immagine che ho riportato qui sotto, con l’unica eccezione per Machine Name che andrà compilato con l’indirizzo IP del vostro Raspberry Pi.

mathematica-raspberry-finestra5 — Fig.23: Compilami!

Cliccate su OK, a questo punto tornerete alla finestra precedente, alla quale si è aggiunta la nuova voce Raspberry Pi. Cliccate su OK e tornerete a Mathematica.

A questo punto non resta che decidere quale kernel utilizzare, quello della macchina locale o quello del Raspberry Pi. Per decidere quale kernel usare andiamo su: Evaluation e poi su Default Kernel e scegliamo la nuova voce Raspberry Pi. Si aprirà una finestra che richiede la password per accedere al Raspberry Pi (a proposito… l’avete cambiata, vero?) e il gioco è fatto!
Se date il comando:$MachineName

otterrete come risposta raspberrypi.

mathematica-raspberry-finestra6 — Fig.24: usiamo il kernel del Raspberry!

Se, a questo punto, eseguite sul vostro PC uno qualunque dei programmini mostrati in precedenza, per esempio utilizzando i LED, vedrete i LED accendersi sul Raspberry.

Mathematica in modalità testuale

Coloro che utilizzano Mathematica professionalmente, in genere, non utilizzano spesso l’interfaccia grafica, se non per visualizzare graficamente dei risultati o fare delle manipolazioni su dati già calcolati.
Questo perchè il kernel, da solo, è infinitamente più veloce e permette, grafica a parte, qualunque calcolo e qualunque elaborazione possibile con Mathematica.
Personalmente ho trovato molto più proficuo il collegamento al Raspberry Pi con Putty in SSH lanciando il kernel in modalità testuale rispetto ad ogni altra soluzione. E’ molto veloce e permette elaborazioni egregie.
Una volta stabilita la connessione SSH con il Raspberry Pi è possibile lanciare il kernel di Mathematica digitando semplicemente:sudo wolfram

mathematica-raspberry-putty1 — Fig.25: Putty on Raspi

A questo punto è possibile, interfaccia grafica a parte, utilizzare tutti i comandi di Mathematica (sono più di 5k). Facciamo qualche semplice calcolo utilizzando il kernel da solo:

mathematica-raspberry-putty2 — Fig.26: Chi l’avrebbe mai detto, DirtyDeeds…

Se volete eseguire in automatico un programma potete creare un file di testo che lo contiene e poi salvarlo con l’estensione .m. Supponiamo di aver creato il file di testo LED.m e volerlo eseguire.

Da linea di comando potete digitare:sudo wolfram -script LED.m

Mentre, se avete già avviato il kernel, vi basterà dare il comando:<< _percorso_\LED.m

Quando avete finito potete uscire con il comando:Quit (Q maiuscola)

Conclusioni

In questo articolo ho cercato di effettuare una panoramica sull’uso di Mathematica e, con la scusa del Lampone, ne ho introdotto alcune funzioni specialistiche, sia per l’uso dedicato al minicomputer, sia per l’uso generale.
Lo dedico a tutti coloro che intendano avvicinarsi a questo programma e, più in generale, al mondo della modellistica.
Che ogni giorno sia una scoperta della bellissima realtà fisica che vi circonda.
Vi auguro di non smettere mai di stupirvi.

Installazione di Mathematica sul Raspberry Pi

Mathematica

Primo sguardo

Il primo comando

Il primo grafico

Un diagramma di Bode

Un diagramma di Nyquist

Un diagramma di Nichols

Risolvere equazioni differenziali lineari alle derivate ordinarie

Parametrizzazioni, animazioni e LPDE

Matrici

Comandi Mathematica per Raspberry PI

Modalità superuser

Un semplice circuito

Leggere lo stato di un pin

Importare immagini dalla telecamera per Raspberry Pi

Mathematica in modalità testuale

Conclusioni

Lascia un commento Annulla risposta