Calculate Probability Mass Function (PMF) with Python

Post Views: 1,251

Probability Mass Function with Python header

The Probability Mass Function (PMF) is a function that associates with each value of a discrete random variable the probability that the variable takes on that particular value. In other words, the PMF provides the probability distribution of a discrete random variable.

[wpda_org_chart tree_id=11 theme_id=50]

The Probability Mass Function

specification that the variable can take on. PMF satisfies the following properties:

The probability associated with each value is non-negative: $P(X=x) \geq 0 [/laetx] for all [latex] x$ .
The sum of the probabilities for all possible values is equal to 1: $\sum P(X=x) = 1$ over all values of $x$ .

The PMF provides a complete representation of the probabilities associated with the various outcomes of a discrete random variable. It is essential for calculating probabilities of complex events, such as joint or conditional events, using probability rules such as the sum rule and the product rule. PMF also allows you to make predictions and better understand the behavior of random variables in a wide range of contexts, from queuing theory to statistical modeling.

In summary, the PMF is a fundamental function in discrete probability distributions, providing a detailed description of the probabilities associated with each possible outcome of a discrete random experiment.

Examples of PMFs

The fair dice

A common example of a PMF is the probability distribution of a standard six-sided die. If (X) represents the result of the die roll, the PMF would be:

$P(X=x) = \frac{1}{6}$

for each $x = 1, 2, 3, 4, 5, 6$ .

The Binomial Distribution

The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed sequence of independent trials, each with a constant probability of success (p).

The Probability Mass Function (PMF) of the binomial distribution is given by the following formula:

$P(X = k) = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}$

Where:

(X) is the random variable representing the number of successes in the sequence of attempts.
(k) is the number of successes we are considering.
( n ) is the total number of attempts.
(p) is the probability of success in any single attempt.
$(1-p)$ is the probability of failure in any single attempt.
$\binom{n}{k}$ represents the binomial coefficient, which indicates the number of ways in which ( k ) successes can occur in ( n ) trials and is calculated as $\frac{n !}{k!(n-k)!}$ , where $n!$ is the factorial of ( n ).

The PMF of the binomial distribution gives the probability that a specific number of successes will occur in a sequence of independent trials with a constant probability of success (p). This distribution is useful in a variety of contexts, such as in calculating the probabilities of success or failure in repeated experiments, in the context of hypothesis testing, or in studying processes involving binary outcomes.

The Poisson Distribution

The Poisson distribution is a discrete probability distribution that describes the number of rare events that occur in a certain interval of time or space, given an average rate of occurrence ( \lambda ).

The Probability Mass Function (PMF) of the Poisson distribution is given by the following formula:

$P(X = k) = \frac{e^{-\lambda} \cdot \lambda^k}{k!}$

Where:

(X) is the random variable representing the number of events that occur in the time or space interval.
(k) is the number of events we are considering.
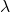$\lambda$ is the average rate of occurrence of events in the specified interval.
(e) is the Naper number, approximately (2.71828).
$k!$ represents the factorial of ( k ), that is, the product of all positive integers from 1 to ( k ).

The PMF of the Poisson distribution gives the probability that a specific number of rare events will occur in a given interval of time or space, given a certain mean of occurrence ( \lambda ). This distribution is often used to model events such as customer arrivals in a store, calls in a call center, errors in a production process, and in general any phenomenon that occurs randomly and rarely in time or space.

Let’s implement the example PMFs in Python

Now let’s look at the three examples of discrete distribution seen previously and develop the same number of example codes in Python. You will be able to use and modify these codes to better understand the functioning of discrete distributions and their PMFs.

The Fair Dice

For this simple example, to generate the PMF simply use the NumPy library. Let’s see the code.

import numpy as np
import matplotlib.pyplot as plt

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, poisson

# PMF of the fair dice
num_dice_faces = 6
dice_probability = np.ones(num_dice_faces) / num_dice_faces
dice_values = np.arange(1, num_dice_faces + 1)

plt.figure(figsize=(8, 5))
plt.bar(dice_values, dice_probability, color='skyblue')
plt.title('PMF of the fair dice')
plt.xlabel('Dice value')
plt.ylabel('Probability')
plt.xticks(dice_values)
plt.grid(True)
plt.show()

In this code, we are considering a fair dice with 6 sides. The variable num_faces_die represents the number of faces of the die. We initialize a die_probability array with uniform probabilities 1661 for each face of the die. The die_values array contains the possible values the die can take, from 1 to 6. Using matplotlib, we create a bar graph representing the PMF of the fair die, with the die values on the x-axis and the corresponding probabilities on the y.

Running the code will give you a graph like the following, which corresponds to the PMF of the fair die.

The binomial distribution

In this case, more complex than the previous one, we will make use of the specific scipy stats module which already has all the tools for working with binomial distributions defined within it, including the calculation of the PMF via the binom.bmf() function.

from scipy.stats import binom

# PMF of the binomial distribution
num_trials = 10
success_probability = 0.5
binom_values = np.arange(0, num_trials + 1)
pmf_binom = binom.pmf(binom_values, num_trials, success_probability)

plt.figure(figsize=(8, 5))
plt.bar(binom_values, pmf_binom, color='lightgreen')
plt.title('PMF of the binomial distribution (n=10, p=0.5)')
plt.xlabel('Number of successes')
plt.ylabel('Probability')
plt.xticks(binom_values)
plt.grid(True)
plt.show()

In this code, we are considering a binomial distribution with 10 trials and a 50% probability of success on each trial. The num_attempts variable represents the total number of attempts. The success_probability variable represents the probability of success in each attempt. The binom_values array contains the possible numbers of successes, from 0 to 10. We use the binom.pmf() function from the scipy.stats module to calculate the PMF of the binomial distribution. Let’s create a bar graph using matplotlib to display the PMF of the binomial distribution, with the number of successes on the x-axis and the corresponding probabilities on the y-axis.

Probability Mass Function binomial distribution

The Poisson distribution

Also in this case, like the previous one, we will make use of the specific scipy stats module which already has all the tools for working with poisson distributions defined within it, including the calculation of the PMF via the poisson.bmf function.

from scipy.stats import poisson

# PMF of the Poisson distribution
mean_rate = 3
poisson_values = np.arange(0, 15)
pmf_poisson = poisson.pmf(poisson_values, mean_rate)

plt.figure(figsize=(8, 5))
plt.bar(poisson_values, pmf_poisson, color='salmon')
plt.title('PMF of the Poisson distribution (&lambda;=3)')
plt.xlabel('Number of events')
plt.ylabel('Probability')
plt.xticks(poisson_values)
plt.grid(True)
plt.show()

In this code, we are considering a Poisson distribution with an average rate of 3 events. The average_rate variable represents the average rate of occurrence of events. The poisson_values array contains the possible numbers of events, from 0 to 14 (chosen arbitrarily for display). We use the poisson.pmf() function from the scipy.stats module to calculate the PMF of the Poisson distribution. Let’s create a bar graph using matplotlib to display the PMF of the Poisson distribution, with the number of events on the x-axis and the corresponding probabilities on the y-axis.