La Statistica Inferenziale è la branca della statistica che si occupa di fare affermazioni e prendere decisioni sulla popolazione in base a un campione rappresentativo di dati. Mentre la Statistica Descrittiva si concentra sulla presentazione e sull’analisi dei dati, la Statistica Inferenziale estende il suo sguardo, cercando di trarre conclusioni che vanno al di là di ciò che è immediatamente osservabile.
L’obiettivo principale della Statistica Inferenziale è fare inferenze sulla popolazione sulla base di un campione rappresentativo di dati. Questo processo coinvolge la formulazione di ipotesi, la raccolta di dati, l’applicazione di tecniche statistiche e la trazione di conclusioni che vanno oltre i dati osservati.
[wpda_org_chart tree_id=7 theme_id=51]
Il Ruolo della Statistica Inferenziale
Una delle tecniche fondamentali della Statistica Inferenziale è l’Hypothesis Testing (Test di Ipotesi), che ci consente di valutare se le differenze osservate tra i gruppi di dati sono il risultato del caso o rappresentano una differenza reale. Questo processo coinvolge la formulazione di un’ipotesi nulla (H0) e un’ipotesi alternativa (H1), seguito da test statistici per determinare la significatività delle differenze osservate.
L’Analysis of Variance (ANOVA), o Analisi della Varianza, è un’estensione di queste tecniche. Invece di confrontare solo due gruppi di dati, l’ANOVA valuta le differenze tra tre o più gruppi. Questa tecnica si basa sulla variabilità dei dati all’interno e tra i gruppi, consentendo di determinare se esistono differenze significative tra almeno due gruppi.
Un’altra tecnica chiave è la Regressione, che analizza la relazione tra una variabile dipendente e una o più variabili indipendenti. La Regressione Avanzata può essere utilizzata per modellare relazioni complesse e fare previsioni basate su tali modelli.
L’Importanza della Dimensione del Campione
La dimensione del campione gioca un ruolo cruciale nella Statistica Inferenziale. Mentre un campione più grande tende a fornire stime più accurate dei parametri di una popolazione, è importante bilanciare la dimensione del campione con le risorse disponibili e la precisione richiesta per le inferenze.
Innanzitutto, una dimensione del campione più ampia contribuisce a ottenere stime più precise dei parametri di una popolazione. La media campionaria, ad esempio, si avvicina maggiormente alla vera media della popolazione quando il campione è più grande, garantendo una maggiore accuratezza nei risultati.
La stabilità delle stime è un altro aspetto chiave. Campioni più grandi tendono a generare stime più robuste, meno influenzate dalle variazioni casuali presenti nei campioni più piccoli. Questo garantisce una maggiore coerenza nelle conclusioni tratte dai dati.
La rappresentatività è un concetto cruciale: un campione più grande ha una maggiore probabilità di riflettere accuratamente la variabilità presente nella popolazione. Questo è particolarmente importante quando si intendono generalizzare i risultati del campione all’intera popolazione.
Il Teorema del Limite Centrale costituisce un pilastro fondamentale della statistica inferenziale. Esso afferma che, indipendentemente dalla forma della distribuzione della popolazione di partenza, la distribuzione delle medie di campioni casuali di dimensioni sufficientemente grandi tende ad avvicinarsi sempre più a una distribuzione normale. In altre parole, il teorema del limite centrale fornisce una base teorica essenziale per giustificare l’uso della distribuzione normale in molte inferenze statistiche.
L’errore standard, inversamente proporzionale alla radice quadrata della dimensione del campione, diminuisce con campioni più grandi, garantendo stime più accurate. La potenza dei test statistici, ovvero la capacità di rilevare un effetto vero, aumenta con la dimensione del campione, migliorando la capacità di identificare effetti significativi.
Tuttavia, è essenziale sottolineare che una dimensione del campione più grande non costituisce una soluzione automatica a tutti i problemi. La scelta della dimensione del campione deve essere bilanciata attentamente con le risorse disponibili e la precisione richiesta per le specifiche inferenze che si stanno facendo. In alcune circostanze, la raccolta di un campione più grande potrebbe essere impraticabile o costosa, richiedendo un’attenta valutazione delle strategie alternative.
Il Complesso Equilibrio tra Rischio e Certezza
La Statistica Inferenziale implica inevitabilmente un equilibrio tra rischio e certezza. In particolare, ci si riferisce alla delicata bilancia tra il rischio di commettere errori di tipo I e di tipo II nei test di ipotesi. Questo concetto è particolarmente evidente quando si definisce il livello di significatività 
e la potenza del test.
- Errore di Tipo I (Falso Positivo): Questo si verifica quando si rifiuta erroneamente un’ipotesi nulla vera. Riducendo il livello di significatività 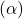, cioè la probabilità di commettere un errore di tipo I, si riduce il rischio di affermare erroneamente l’esistenza di un effetto quando non c’è.
- Errore di Tipo II (Falso Negativo): Si verifica quando si accetta erroneamente un’ipotesi nulla falsa. Aumentando la potenza del test, ovvero la probabilità di rilevare un effetto vero, si riduce il rischio di non rilevare un effetto esistente.
Il dilemma sta nel fatto che ridurre il livello di significatività per diminuire il rischio di errore di tipo I può aumentare il rischio di errore di tipo II e viceversa. Trovare l’equilibrio ottimale dipende dalla specificità del contesto e dalle conseguenze pratiche degli errori.
In molti casi, la scelta del livello di significatività viene stabilita a priori, spesso utilizzando un valore comune come 0.05 o 0.01. Questo determina quanto si è disposti a rischiare di commettere un errore di tipo I. Tuttavia, è essenziale valutare attentamente le conseguenze pratiche di entrambi gli errori e considerare la potenza del test nella progettazione dello studio.
Applicazioni Pratiche della Statistica Inferenziale
Certamente, le applicazioni pratiche della statistica inferenziale sono varie e si estendono a diverse discipline. Ecco alcuni contesti in cui la statistica inferenziale trova ampio impiego:
Medicina e Scienze della Salute:
- Sperimentazioni Cliniche: La statistica inferenziale è fondamentale nella valutazione dell’efficacia di nuovi farmaci o trattamenti attraverso sperimentazioni controllate.
- Studi Epidemiologici: Per analizzare l’incidenza di malattie in popolazioni e identificare fattori di rischio.
Economia e Finanza:
- Analisi dei Mercati Finanziari: Per fare previsioni sulla direzione dei mercati, valutare il rischio e prendere decisioni di investimento.
- Studi di Mercato: Nell’analisi dei dati di mercato per comprendere comportamenti dei consumatori e tendenze.
Industria e Qualità del Prodotto:
- Controllo di Qualità: Per garantire la conformità dei prodotti alle specifiche attraverso la valutazione di campioni.
- Ottimizzazione dei Processi: Utilizzando l’analisi sperimentale per migliorare i processi produttivi.
Ricerca Sociale e Scienze Umane:
- Sondaggi e Indagini: Per estrapolare conclusioni sulla popolazione da un campione rappresentativo.
- Psicologia: Nell’analisi dei dati sperimentali per testare ipotesi su comportamenti umani.
Ambiente e Scienze Naturali:
- Monitoraggio Ambientale: Nell’analisi dei dati relativi a inquinamento, cambiamenti climatici e biodiversità.
- Biologia: Nelle sperimentazioni biologiche e nell’analisi dei dati genetici.
Ingegneria e Tecnologia:
- Affidabilità del Prodotto: Utilizzando la statistica per valutare la durata e l’affidabilità di un prodotto.
- Ottimizzazione dei Sistemi: Applicando tecniche di regressione e analisi sperimentale per migliorare l’efficienza dei sistemi complessi.
Pubblica Amministrazione e Politica:
- Sondaggi Politici: Per predire i risultati delle elezioni e comprendere le preferenze degli elettori.
- Pianificazione Urbana: Nell’analisi dei dati demografici e sociali per prendere decisioni sulla pianificazione del territorio.
Educazione e Ricerca Accademica:
- Valutazione dell’Apprendimento: Utilizzando l’analisi statistica per valutare l’efficacia dei metodi didattici.
- Ricerca Scientifica: Nell’analisi dei dati sperimentali per trarre conclusioni significative.
In ogni settore, la statistica inferenziale gioca un ruolo chiave nel supportare decisioni basate sui dati, contribuendo a identificare modelli, confermare ipotesi e guidare il processo decisionale in maniera informata. La sua applicazione pratica contribuisce a migliorare l’efficienza, la precisione e la validità delle conclusioni tratte da dati complessi.
Conclusioni: Una Guida Necessaria nel Mare della Complessità dei Dati
In conclusione, la Statistica Inferenziale si presenta come una guida fondamentale nella navigazione del mare intricato dei dati. Attraverso l’Hypothesis Testing, la Regressione, l’ANOVA e altre tecniche, offre un mezzo per fare affermazioni informate sulla popolazione basate su campioni rappresentativi. Le sue applicazioni pratiche sono ampie e diversificate, rendendola uno strumento indispensabile per coloro che cercano di prendere decisioni informate e guidate dai dati.
Il nostro viaggio nella Statistica Inferenziale è solo all’inizio. Nelle prossime sezioni di questa esplorazione, approfondiremo ciascuna tecnica, esaminando casi studio e applicazioni reali per acquisire una comprensione più profonda di come questa disciplina possa plasmare il nostro modo di interpretare e utilizzare i dati.